科学家掐指一算——二向箔里应有任意子

小墨曾经给大家介绍过微观粒子的分类。我们说光子是玻色子，电子是费米子，它们的区别在哪里呢？

我们想象一下，让两个全同粒子交换一下位置，这可以通过令其中一个绕着另一个沿顺时针（或者逆时针）转半个圈圈来实现，两个粒子的波函数会产生变化——和原波函数相差一个相位因子。如果相位等于0或者2π的整数倍，就是玻色子；如果是π的奇数倍，就是费米子。

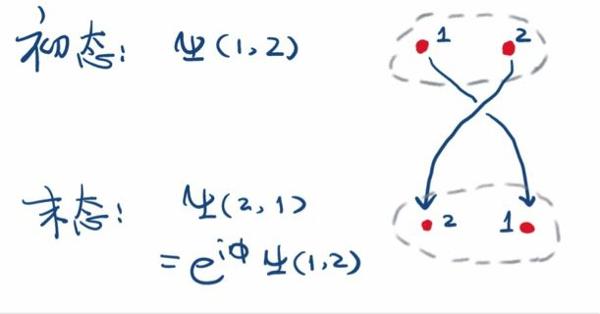
交换两个微观粒子会产生一个整体相位因子Φ 

但是科学家发现，在二维情况，由于一些拓扑学上的原因，这个相位可能取0到π之间的任意数值（甚至可能是一个矩阵），既然这种粒子这么任性，干脆叫它“任意子”好了。

虽然数学上有合理性，但是任意子究竟存不存在，这是个问题。好在，后来人们在一些低温、强场的二维体系（比如分数量子霍尔态）里观察到了任意子的迹象——系统从基态（真空态）跃迁到低激发态的过程，可以看做是准粒子产生的过程，而这种准粒子的统计行为，符合任意子的性质。

实验还发现，这种元激发产生的任意子有一个特性，它带有分数电荷。这个分数是多少，直接跟材料的拓扑性质有关。所以人们一直希望能直接观察到这个拓扑元激发和分数电荷的情况，这样，对任意子的了解才会更直接。

任意子还可以做量子计算！

虽然实验上，对任意子的了解还不十分清楚，但是，科学家还是敏锐地发现，任意子系统是实现量子计算的好材料。为什么这么说呢？

现在,请你跟着小墨一起回忆一下，经典计算机的原理怎样的。

首先，我们用高、低电平代表0和1，再用逻辑电路按照一定程序对比特位进行逻辑操作，最后输出结果，这样就实现计算。

那么，对于量子计算机我们可以类似地理解这个过程。只不过，经典比特变成了量子比特，它可以处在0和1的叠加态上。然后我们对量子比特进行一个量子的操作，最后对末态进行测量，得到结果。

在物理体系的选择上，科学家们做了很多种不同的尝试。比如，电子的自旋、光子的偏振、约瑟夫森结的二能级系统，都可以表示为两个态的叠加，从而作为量子比特。但是，它们都有一个比较大的问题，就是很难在计算过程中一直保持相干性。而没有了相干性，量子计算就没有了优势。

在克服这个问题的道路上，有一种方法自成一派，就是拓扑量子计算。

小墨在朋友中强行科普“拓扑量子计算”的时候，所有人的表情似乎都在说：字都认识，连在一起不知道啥意思。好吧，小墨就分开说说这几个字。

何为“拓扑量子计算”

我们先来认识一下什么叫拓扑。

拓扑你可以理解为某些性质的不变性。比如说，最直观的就是几何上的不变性——一个甜甜圈和一个咖啡杯，虽然长得很不一样，但是从拓扑学的角度上，两者完全一样，都是有一个洞，所以咖啡杯可以通过连续形变，变成甜甜圈的模样。除了几何上的理解以外呢，物理上有些系统也有类似的规律——不论你怎么操作它，或者系统中的个体怎么变化，有一些性质是整体上不变的，我们就叫它拓扑系统。

那么什么叫量子计算呢？我们前面说过，我们需要编码一个逻辑量子比特，这个量子比特跟经典比特最大的不同是，要可以实现0和1两种状态的叠加；然后，还需要对量子比特进行幺正变换，也就是操作或者说计算；最后，对于结果要可以测量，也就是读出。

当科学家把量子计算和拓扑放在一起，他们是想干嘛呢？他们是希望，利用系统某些不变性，实现最强大的容错功能，我们不再需要小心翼翼得保护每一个脆弱的自旋，整个体系自己就牢牢守住某种性质不变，只要外界干扰不特别厉害，系统都不会被扰动。

一句话，科学家想要构建一种特殊的状态，这种状态受拓扑保护，不那么容易受到周围噪声的干扰，可以很好的保持相干性。

这种天然就具有抗扰动能力的量子计算，无疑对科学家有着特别的吸引力，借助神奇的任意子，科学家就有可能将其变为现实。

任意子是一种准粒子，按照拓扑荷的不同，可以分为几种类型。任意子未被激发出来的状态叫做基态，由于基态可以是简并[1]的，这两个简并的态通过叠加，就可以编码一个量子比特；接下来，通过某些手段激发出任意子，利用任意子系统总拓扑荷不变的性质，拖拽任意子进行交换，也就是形成编织，然后让系统回到基态空间，这也就对基态执行了幺正变换；最后，对终态进行测量，提取计算结果。

对这个准粒子系统来说，基态和激发态之间必须要有一个不小的能隙，这样一来，只要外界扰动不太大，都不会导致系统跃迁到激发态，从而避免引进错误。

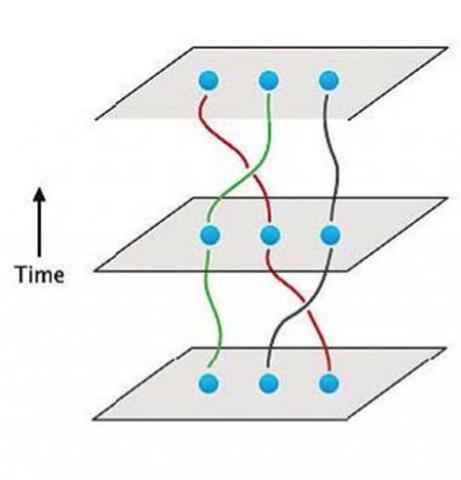
任意子的编织

科学家让准粒子由虚变成实

你读到这里，是不是感觉“听上去很美”？是的没错，任意子到底只是一种准粒子，在大多数人看来，它只是理论体系上的一种描述手段，并不像电子、光子那样天然就存在于我们身边。人们至今还没有在天然的物质体系中找到过任意子。

那么，我们人为地构造一个任意子系统，可行吗？

2003年，Kitaev提出拓扑量子计算，在他的理论方案里，他设计了一种人造自旋网格模型，由自旋为1/2的粒子构成网格，这些粒子之间存在特殊的相互作用，形成一个拓扑系统，这个体系的元激发就对应任意子，基态和激发态之间存在能隙，可以对局域的扰动免疫。

可是，并不是我们随便找几个自旋1/2的粒子排成网格就行的。因为，我们不但需要这几个粒子之间存在相互作用，还得保证这些相互作用是Kitaev模型里描述的那些。实验科学家尝试过一些方法，但是都没有满足Kitaev模型拓扑物态需要的相互作用。

在Kitaev模型里，需要粒子之间的相互作用为四体相互作用，可是难就难在，通常情况下，四体相互作用是一个四阶小量，跟两体相互作用比起来，像一个小矮人，直接看到太难了。怎么办呢？只能把两体相互作用这个大个子给赶走，不让它出现在这里，这样，就只剩下清清楚楚的四体相互作用了。

最近，针对这个难题，中科大的潘建伟研究团队给我们带来了好消息。该团队的科学家们，搭建了新的调控平台，他们构造了人工的量子晶体，用来完美地囚禁和操控超冷原子。原子被放置在二维的光晶格中，光晶格的极化势经过特殊设计，形成了有效磁场梯度，抑制了晶格中存在的两体相互作用这个巨人，这时，小矮人——四体相互作用成为了这个系统最主要的相互作用，就像Kitaev模型里要求的那样。最终，科学家成功操控光晶格中约800个超冷原子，同时产生了约200组四原子自旋纠缠态。

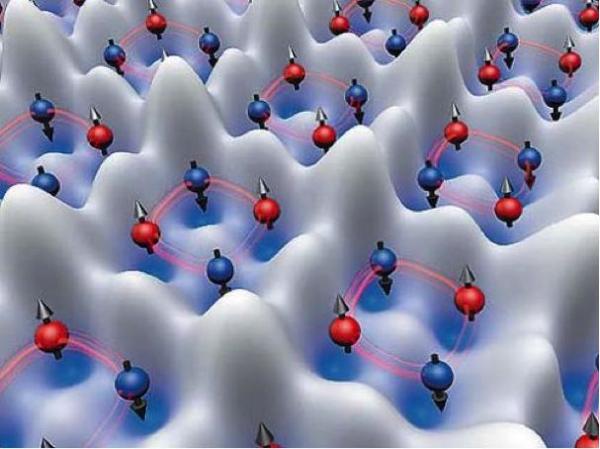
光晶格中的原子自旋纠缠

那么，在这样的相互作用下，晶格中超冷原子会有怎样的动力学行为呢？在高分辨的原位光吸收成像技术的帮助下，科学家首次观测到了四体环交换相互作用，并且与理论预言中任意子激发的能隙符合得很好，这明确无误地展示了四体相互作用占主导的情形。

另外，既然任意子是由这个四原子体系激发出来的，科学家们将四个原子化身为提木偶的线，通过微波反转原子自旋的方法，实现了任意子之间的编织交换过程，实验结果也明明白白的显示出，任意子交换一次，会产生1/2 π的拓扑相位，自此，Kitaev模型第一次从理论走变成了现实。

当然，这个小小的四原子晶格只是任意子激发的基本单元，在验证了这个基本单元的可行性之后，科学家会想办法将这些小单元连接成一个更大的系统。但无论如何，这个由四个超冷原子组成的小单元的实现，都是拓扑量子计算重要的一步，拓扑相进行量子计算和量子模拟终于再也不是纸上谈兵，科学家有信心沿着这个方向走得更远，直到它们的最终实现。

[1]简并：在量子力学里，处于同一能级的粒子，可以有若干种不同的状态，该能级状态就是简并态，就像住在同一楼层的不同的人。