近日,哈佛大学的Markus Greiner团队,Mikhail D. Lukin团队和麻省理工大学的Vladan Vuletic团队等人联合发布了一篇文章[1],展示了他们用中性原子体系研发的48个逻辑量子比特的量子计算原型机,并且展示了对这些逻辑量子比特的逻辑操作,该文章于2023年12月6日发表在《自然》(Nature)杂志上。
48个逻辑量子比特或许听起来并不多,但实现对48个逻辑比特的操作背后是对280个原子的精确操控和探测,可以说这是人类第一次构建规模如此之大的可操控的逻辑层面量子系统,业内因此引发了广泛讨论,多数人认为,这一重大飞跃标志着开发实用的容错量子计算机一个里程碑式的进展。那么,何为逻辑量子比特?为什么对逻辑量子比特的逻辑操作如此重要呢?中性原子量子计算将会是通用量子计算最终的方案吗?下面我们将从量子纠错、原子比特、光镊阵列几个方面带大家来了解下这篇工作的前因后果。
随着技术的发展,目前量子计算已经在几个特定的问题上证明了量子优越性,然而,在进一步扩大规模,实现通用量子计算的道路上,目前主要面临的挑战之一是量子比特极易受到噪声的影响。有些科学家们估计,执行一个大规模,有实用意义的量子算法可能至少需要操控量子比特的出错率在1×10-10以下,而目前最好的量子系统执行量子逻辑纠缠门的错误率也大于1×10-4[2],离目标值还相差甚远。这样的出错率看起来很小,但是只要规模稍大,计算步骤稍多,最后的结果正确的可能性也极低。
一个解决此问题的方案是量子纠错,把多个物理量子比特编码成一个逻辑量子比特来降低出错率。这是怎么做到的呢,回顾经典的信息理论中,我们经常可以通过增加信息的冗余来降低信息的出错率,比如单个比特0如果有p的概率出错翻转到1,我们可以把0复制三份变为000,那么只要不是三个比特中有大于等于两个比特同时出错,我们总还是可以正确地把它纠正回来,当单比特错误率p小于一定值时,我们就总能得到更低的逻辑出错率。这样“用空间换取准确性”的思路对量子比特也同样适用,只不过由于量子比特不可克隆,有相位错误等特点,量子纠错码不能是简单地复制多份,需要精心的设计和构造。图1:单个比特用纠错码理论的纠错过程
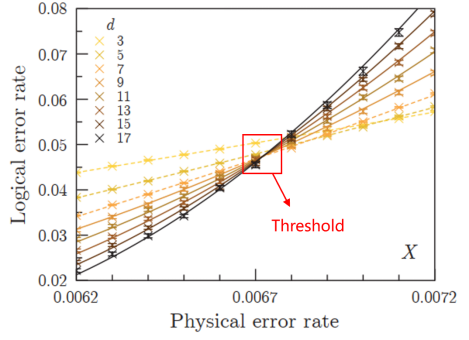
然而,即便有量子纠错码的帮助,实现1×10-10量级的出错率仍是困难的,这是因为逻辑量子比特的设计大大增加了对物理量子比特数量的需求(overhead),而且要想逻辑量子比特表现得比物理量子比特更好,本身要求物理量子比特的出错率低于一个特定的值,否则只会“越纠越错”。在大规模的量子纠错中,这个从“越纠越错”到“越纠越好”的特殊转变点被称为“阈值”(threshold),它指的是仅当物理量子比特的出错率低于这个值的时候,我们才能通过不断增加纠错码的码距来指数级地压缩逻辑量子比特的出错率。目前一些主流的量子纠错码的阈值大约在0.6%~1%左右[3]。图2:模拟得到的surface code的阈值,此处为深度6的线路[3]
虽然我们知道了,构造逻辑比特是一个可行的纠错方案,但在具体的实现上,还不知道哪种技术路线能做到最好,目前,有许多的技术路线在相互竞争,比如光子,超导芯片和离子阱(就像上个世纪可以选择用电子管、晶体管来作为构造计算机的候选者)。而此次哈佛报道的工作,使用的是中性冷原子阵列。经典计算机可以用逻辑与(And),逻辑非(Not)和逻辑或(Or)三个基本逻辑操作构建出任意复杂逻辑运算。类似的,量子计算机可以通过单量子比特旋转和双量子比特纠缠门组合出任意量子操作,只有能实现这种功能,量子计算机才能被称为通用的(Universal)。在中性原子量子计算里,量子比特被编码在原子内电子的两个能级上。使用引起两能级之间跃迁的激光去操纵这个电子的状态,就能达到给这个量子比特做单比特门的效果。而对于两个原子之间的双量子比特纠缠门,怎么去实现呢?这就要通过将原子激发到里德堡态,从而让它们之间产生强烈的相互作用。里德堡原子是电子处于很高能级的原子,它的电子云距离原子核较远,甚至能达到微米量级。所以距离较近的两个里德堡原子会产生电子云的交叠,从而产生强烈的排斥。可以想象,对于一堆原子团,我们不能把间距小于某个特定距离d的两个原子同时激发到里德堡态——这种现象被称作“里德堡阻塞”效应,直观地说,如果原子离的太近,一个原子的激发会把另一个原子“挤”下去,就像会场中相邻的两个座位只有一个人能把手放在中间的扶手上一样,如同图3所示。
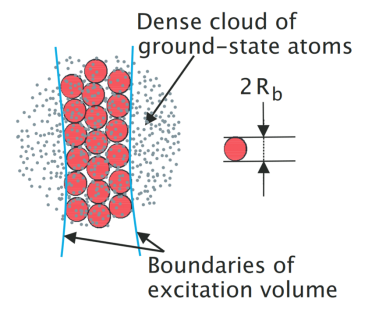
图3:灰色圆点是原子,红色圆是产生里德堡阻塞的距离d。图中红色圆中心的原子被激发到了里德堡态,故红色圆中的其他原子都不能被激发到里德堡态,否则将会因为强烈排斥而被推走。这就是里德堡阻塞效应。[4]
可以看到,只要将原子靠得很近,就可以实现里德堡阻塞。于是,我们可以通过调控原子间距,把想要做纠缠门的一对原子间距拉进,不需要做纠缠门的原子间距拉远分开——这样我们能在原子阵列中做任意的多对双量子比特纠缠门。
通过以上的实验方法,目前在中性原子上做单比特门(99.91%)、双比特门(99.5%)[5]都达到了很高的保真度。正如之前所说,当我们拥有了任意的单比特操作,以及里德堡阻塞的双量子比特纠缠门后,我们就能组合出任意的量子操作,原理上可以进行复杂运算。现在你知道了,任意量子操作的基本单元之一——双量子比特纠缠门,是通过里德堡原子之间的相互作用实现的,而相互作用与原子间距密切相关。那么,为了可以控制原子间相互作用的开与关,我们需要一个工具去控制原子的排列和移动,在中性原子体系中,实现这项功能的通用方法是光镊阵列。早在1986年Arthur Ashkin和朱棣文就实现了用光镊捕获原子[6],其原理是利用光场产生的耦极力把原子束缚在光束聚焦的中心,这个过程就像是把原子用光束作为镊子夹起来了一样。
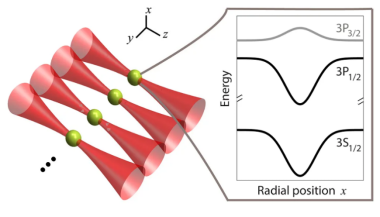
图4:用红光形成的光镊阵列,每个光镊的中心夹着一个原子,右图的曲线代表在光束聚焦的中心有一个能量最低点,原子因此被束缚在此势阱中。
实验人员通过声光器件去连续改变光镊的方向,这样就实现了光镊夹着原子任意移动。用多束这样可排列的光束组成阵列,我们就可以对原子阵列像提线木偶一样摆出我们任意想要的二维形状。

图5:用光镊阵列操控原子的移动编码逻辑量子比特的过程。控制需要做双量子比特纠缠门的一对原子移动到一起,再打入激光,可以实现多对原子的并行双比特门操作[1]。

图6:Lukin团队于2020年展示的工作,通过光镊阵列操控原子重排,他们甚至实现了用原子玩《超级马里奥》,这在当时也是轰动整个领域的工作[7]。
基于光镊阵列巨大的灵活性,中性原子体系量子计算机有许多优点:
第一, 通过提升光镊光总功率和更多的分光,原则上可以实现任意多的光镊阵列,这使中性原子量子计算机有强大的可扩展性。第二, 通过移动光镊可以将原子摆成任意的图案,使中性原子量子计算机轻松实现多对量子比特的并行操作而互不干扰。第三, 实验证明,移动光镊中的原子并不会造成原子相干性的损失,原子在光镊中的寿命也在秒量级左右。这样的特性使得我们可以用不断移动光镊的方法实现复杂的量子线路,为实现实用量子算法奠定了基础。基于光镊平台的特性,Lukin团队结合了之前探索的诸多原子操控技术,实现了这次意义非凡的进步。这次工作最大的亮点莫过于实现了可执行逻辑线路级别模拟的量子系统。之前人们在量子纠错领域的研究还处在研究1到2个逻辑量子比特的性能表征,而这次,研究人员实现了制备和操控48个逻辑量子比特执行线路级的任务,用分区的方法从架构层面研究量子计算机,这远远超过了其他平台上容错量子计算的研究水平,是靠近制造出通用性的容错量子计算机的一大步。
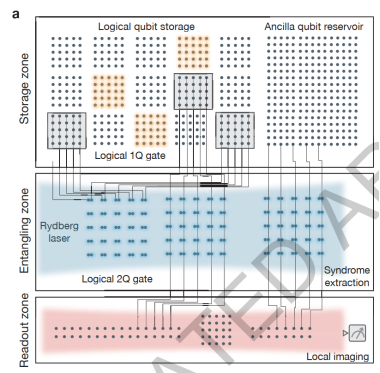
图7:该工作把原子阵列分成了多个区域完成逻辑操作,分别有储存区,纠缠门区和读取区,这样的分区初具量子计算机架构的雏形[1]。
该实验首先研究了扩大量子纠错码的码距对整体线路逻辑错误率的影响。实验对比了码距为3,5,7的纠错码,观察到了随着码距增大,整体线路的逻辑错误率呈下降的趋势,这说明此系统对单个量子比特操控的错误率接近阈值(threshold),因此只要继续扩大系统的规模实现更大的码距,我们有希望能实现更低的逻辑出错率。
之后,实验分别用中性原子体系结合量子纠错理论演示了容错的逻辑算法,逻辑线路和量子模拟。几组实验均观察到了纠错后的结果要比不纠错的结果保真度更高,更接近理论计算的准确值,这表明量子纠错是有效的,的确可以提高量子计算机的可靠性。总而言之,此工作不仅当前在中性原子系统上实现了多个指标相对于之前量子系统的遥遥领先,展示了多个在以往的系统上无法完成的线路和任务,还展现了中性原子体系进一步的可扩展性。作者预期,通过进一步加大光镊的激光功率和优化控制系统,未来几年内可以实现10000个物理量子比特的操控,这将大大加速用量子计算机解决有意义的实际应用问题的进程。回顾历史,最早的纠错编码理论由Richard Hamming(理查德·海明)和Claude Shannon(克劳德·香农)等人提出[8],在经典计算机初期,那时的计算机还是一个由堆满房间的真空管组成的庞大巨兽。当时的真空管出错率也很高,Von Neumann(冯·诺依曼)类比生物和神经系统,思考如何才能基于这些“不可靠”的基本元件构成一个“可靠稳定”的整体,在计算机上发展了基于“用信息冗余换取信息稳定性”的纠错编码理论,提出了容错计算的阈值(threshold)理论[9]。就像我们的DNA在复制过程中其实经常出现碱基配对错误,但仍然准确地记录着我们全部的遗传信息,稳定地控制着蛋白质的合成,人们猜想这是归功于DNA中含有大量无效的片段作为冗余,使DNA复制具有了很强的容错性。时至今日,为了对抗量子计算机中的噪声,人们把纠错编码用于量子计算领域,修改并发展为量子纠错码。此方法最开始由Peter Shor,Andrew Steane和Alexei Kitaev等人提出,经过了十几年,相继在离子阱、超导芯片等体系上实现了一系列里程碑式的实验进展。如今,在中性原子体系上,科学家把纠错这件事儿又往前推进了一大步,并展现出了更清晰的未来技术路径。再看未来,最终,低成本且稳定可靠的通用量子计算机会在中性原子体系上依靠量子纠错码理论实现吗?这还需要时间的检验。毕竟历史的走向总是出乎当时所有人的意料,像Von Neumann(冯·诺依曼)提出容错计算阈值理论后的几年时间后,晶体管的发展就让计算机的出错率达到了低于1×10-14量级,几乎可以忽略不计,人们发现不再需要纠错理论也能使计算机完成大规模的复杂计算。或许某天人们也会发现属于量子计算的“晶体管”,那将会带来一场新的革命,改变整个领域的发展路线。码距:指的是多少个比特发生错误会引起无法纠正的逻辑错误,反映了纠错码能纠正错误的数量,比如上述把一个比特复制三份的重复码(repetition code)的码距为 3,因为当000一起发生错误变为111,此时由于111代表逻辑1,这样的错误无论如何不能被探测和纠正。
[1].Bluvstein, et al. Logical quantum processor based on reconfigurable atom arrays[2]. R. Srinivas, S. C. Burd, H. M. Knaack, et al. High-fidelity laser-free universal control of trapped ion qubits. Nature. volume 597, pages 209–213 (2021)[3].Ashley M. Stephens. Fault-tolerant thresholds for quantum error correction with the surface code. Phys. Rev. A 89, 022321.[4].Saffman, Quantum information with Rydberg atoms. RevModPhys.82.2313[5].Evered, et al. High-fidelity parallel entangling gates on a neutral atom quantum computer. arXiv:2304.05420.[6].A Ashkin, et al. Observation of a single-beam gradient force optical trap for dielectric particles. Optics letters, 1986.[7].Ebadi, et al. Quantum phases of matter on a 256-atom programmable quantum simulator. Nature volume 595, pages227–232 (2021)[8]. R. Hamming. Error detecting and error correcting codes. Bell System Technical Journal. (1950)[9].Neumann J. Von, Probabilistic Logics and the Synthesis of Reliable Organisms From Unreliable Components. (1956)