量子纠缠，相信墨子沙龙的读者们早就不陌生了。2022年诺贝尔物理学奖授予量子纠缠的相关研究，更让它刷屏了每个人的朋友圈，飞入寻常百姓家。所谓量子纠缠，它说的是，在量子世界，粒子之间可以具有一种奇特的联系，而任何经典物理理论都无法描述这种关联。量子力学的奠基人之一薛定谔就说过：“纠缠是量子力学的精髓，正是它使得量子力学和经典物理的思维方式彻底分道扬镳。”（推荐观看“量子纠缠：粒子间鬼魅般的关联 | 量子微课堂”）

说起量子纠缠，你脑海中是不是马上浮现出了上面类似的画面，或者是：

量子纠缠的示意图（来自Quanta Magazine）

这些图像显明地表现出，相隔遥远的两个粒子通过千丝万缕的神秘联系而绑在一起，它们的行为不再独立，而是彼此“同步”，组成了一个整体：一个粒子状态的改变会瞬间影响另一个粒子的状态。是不是简单且奇妙？

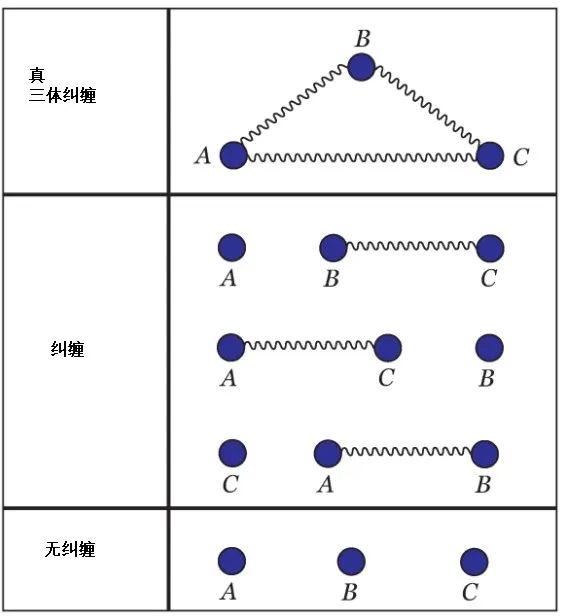
大自然比我们想象的还要有意思，纠缠不仅仅限于两个粒子之间，多个粒子的纠缠更复杂、也更有意思，有丰富的内涵值得去探索！这就是多体量子纠缠（multipartite entanglement）。

一个多体系统含有很多“粒子”（这里的粒子可以是光子、电子，也可以是原子、超导比特等等），如果其中两个粒子纠缠在一起，那么这是不是一个量子纠缠的多体系统呢？是的，哪怕只有一对粒子纠缠了，这个系统就没办法用任何经典模型来描述，它就是一个纠缠体系。就像，只有一个牛肉粒的牛肉面仍然是红烧牛肉面。不过，我们更喜欢有丰富牛肉的牛肉面。我们也希望实现有着更丰富纠缠的“真·多体纠缠”。

（图片来自网络）

所谓真多体纠缠（ genuine multipartite entanglement），它是这样一种状态：如果我们把一个多体系统任意划分为两部分，不论我们如何划分，划分后的两部分之间都存在纠缠，那么我们就说这是一个真多体纠缠体系。假如把每个粒子比喻为珍珠，把粒子间的纠缠比喻为串联珍珠的丝线，那么，这个项链是联通在一起的，无论我们怎么拉扯摆弄，都无法把项链一分为二。真多体纠缠是最强形式的量子纠缠。

（图片来自网络）

不过，要实现大规模的真多体纠缠，面临着极大的挑战。这既体现在制备上——需要对大规模的量子体系具有极高的操控水平，也体现在纠缠态的验证上——对于如此复杂而精微的纠缠结构，我们如何才能知道我们真的实现了真纠缠呢。很多实验技术和理论认知上的难题都需要攻克。

最近，中国科学技术大学潘建伟、朱晓波、彭承志等组成的研究团队与北京大学袁骁合作，取得了重要突破，他们在66量子比特的“祖冲之二号”超导量子处理器上成功制备和验证了高达51个量子比特的真多体纠缠态，研究工作发表在Nature上。

这一工作大大刷新了之前的量子纠缠世界纪录。之前，利用数字的超导量子门实现的最大真多体纠缠态是12量子比特，而在所有物理体系中实现的最大真多体纠缠态也只有29量子比特。

那么，费这么多心力，为什么要实现大规模真多体纠缠呢？

一方面，对它的研究有助于我们更深入地洞悉量子世界的奥秘：量子世界和经典世界的界限在哪里，量子纠缠的本质是什么……另一方面，在量子信息时代，纠缠还是一种重要而独特的资源，“其价值可以和能量、信息、熵及任何其他基本资源相当”。充分了解它、驾驭它，能给我们带来更安全的通信、更快速的计算、更精密的计量……例如，中国科大研究团队这一工作所实现的是一种被称为“簇态”（cluster state）的多体纠缠态，基于簇态，仅仅通过一系列“测量”就可以实现量子计算，甚至通用量子计算。这被称为“基于测量的量子计算”，是不同于通常的“基于量子线路的量子计算”的一种新型量子计算框架。

研究团队制备和验证了51量子比特的一维簇态和30量子比特的二维簇态。为了达成这一目标，他们将单量子比特门和双量子比特门的保真度分别提升到 99.91% 和 99.05%的精度，利用数字的量子门来实现真多体纠缠态的制备（具体过程见下图）；另外，利用随机保真度估计方法，减少了验证纠缠态所需的测量次数，完成了对纠缠态的验证。

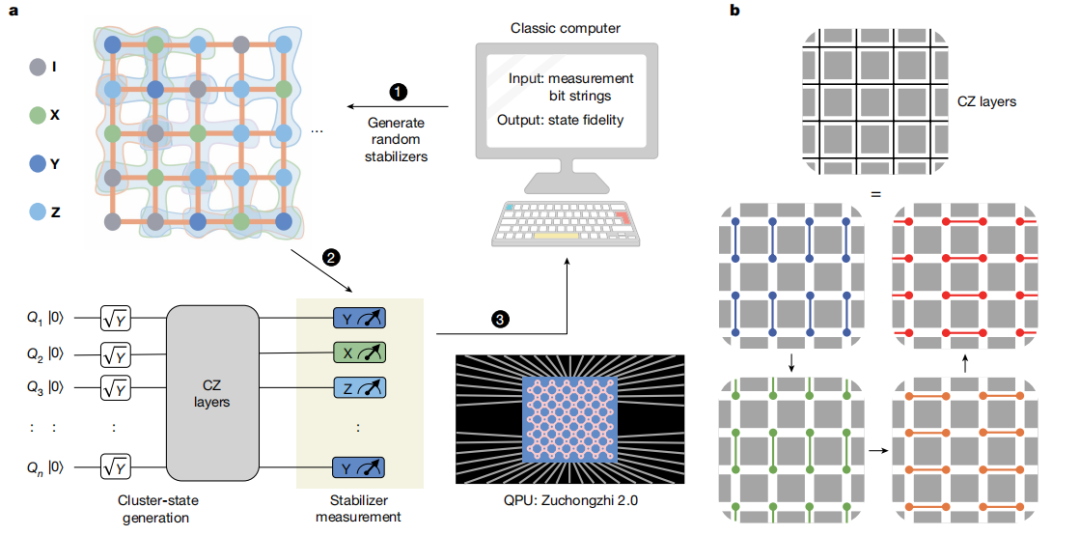
图来自Nature文章：簇态制备和测量过程。在“祖冲之二号”超导量子处理器上，研究人员使用4层CZ操作可以将所有最邻近量子比特对连接在一起制备簇态，接着用经典计算机产生的随机稳定子测量该量子态。同一层内的CZ门可以同时执行。

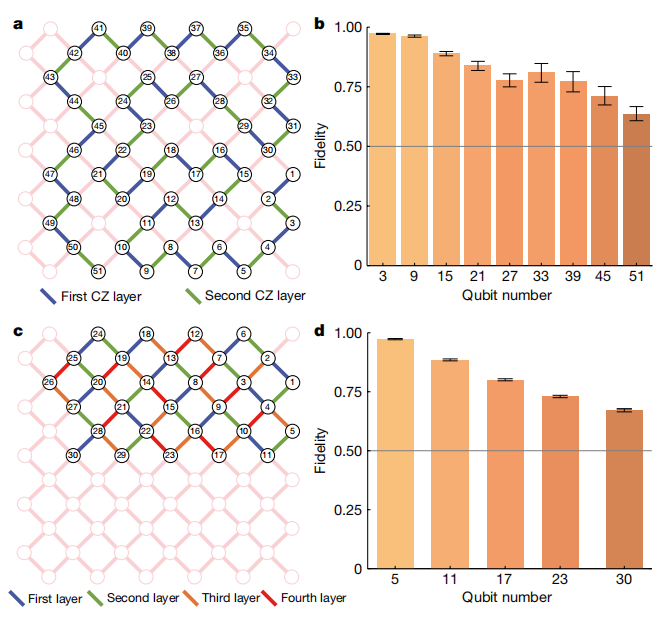
图来自Nature文章：一维（上方图）和二维（下方图）簇态的制备和测量保真度。

什么是簇态？它是一种特殊的图态（graph state）。所谓图，是数学和计算机科学中的一个概念，可以简单的理解为是由一些端点和连接端点的线组成的图案。如果我们用图中端点表示量子比特，而用连线表示一对量子比特间的相互作用，这样，这幅图就表示了一种特殊的多量子比特的纠缠态。这种状态就称为“图态”。如果我们把图限定为方格型结构，那么这种图态就称为“簇态”。

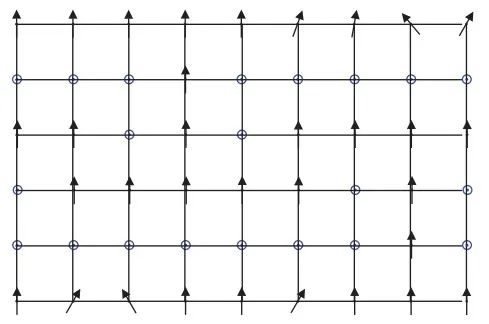
（来自Dan Browne, Hans Briegel.One-Way Quantum Computation）

图态和簇态是量子计算的重要资源。通常的超导量子计算是基于量子线路的，通过量子门操控量子比特来执行计算任务，就像经典计算中，通过经典门操控经典比特来进行运算。然而，量子世界中奇特的“测量”（测量带来量子状态的改变）带来了新的可能，以图态或簇态作为资源，仅通过执行单量子比特测量竟然可以执行各种量子算法，甚至实现通用量子计算。这是一个让人惊奇的发现，我们只需要决定对哪些量子比特进行测量，以及测量的时机和顺序、测量的方式（这些选择往往依赖于上一步的测量结果）就能完成量子计算了！（对于特定的量子计算任务，某种纠缠结构的图态可能最适合这一任务，相比簇态会需要更少的量子比特数和测量次数。但实验上，簇态往往更容易制备，而且重要的是，以簇态作为计算资源，也可以实现通用量子计算。）

利用所制备的簇态，基于测量，研究团队还成功地原理性演示了一种量子计算算法：变分量子本征求解算法，展现了这一量子计算方式的广阔应用前景。

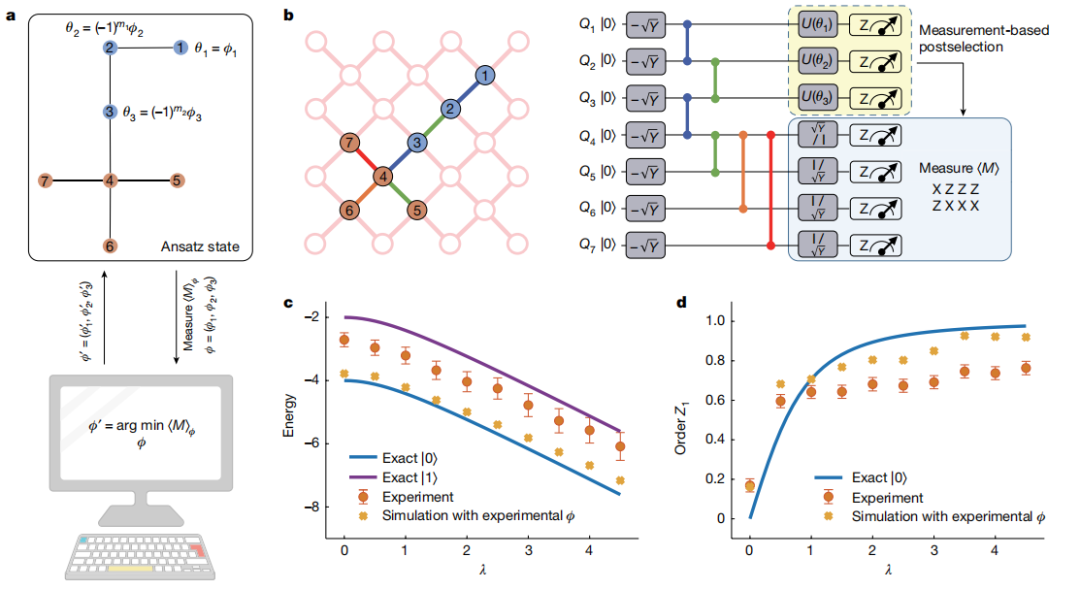
图来自Nature文章：基于测量的变分量子本征求解算法原理验证。对于微扰平面码的本征值求解问题，研究人员选择了7个量子比特先制备到二维簇态，对其中3个比特选择不同的测量角度，根据比特测量结果对剩下4个比特同时测量进行能量计算，完成了微扰平面码本征能量求解的演示。

基于测量的量子计算是一种全新的计算框架，长远看，人们多了一条迈向通用量子计算的路径，近期看，也为针对具体实用问题的量子算法设计提供了新的可能。中国科大对这一量子计算方式的原理性演示，是这条新赛道上的重要一步。

感谢龚明、曹思睿老师对墨子沙龙科普工作的指导和帮助。