美国数学会公布，2021年度“科尔代数学奖”颁给许晨阳教授，以表彰他在代数学领域取得的最新杰出成果，他与合作者们一起发展了K-稳定Fano簇模空间的代数理论，并且用K-稳定性实现了一个研究极小模型纲领中奇点的全新途径。

科尔代数学奖每三年颁发一次，以表彰在过去6年中出现的代数学领域最重要的研究成果。此次奖项授予以下工作：

[1] C. Hacon, J. McKernan and C. Xu, “Boundedness of moduli of varieties of general type,” J. Euro. Math. Soc. 20 (2018), Issue 4, 865–901.

[2] C. Li, X. Wang and C. Xu, “On the proper moduli spaces of smoothable Kähler-Einstein Fano varieties,” Duke Math. J. 168 (2019), 138–1459.

[3] H. Blum and C. Xu, “Uniqueness of K-polystable degenerations of Fano varieties,” Annals of Math. 190 (2019), 609–656.

[4] C. Xu, “A minimizing valuation is quasi-monomial,” Annals of Math. 191 (2020), 1003–1030.

[5] J. Alper, H. Blum, D. Halpern-Leistner and C. Xu, “Reductivity of the automorphism group of K-polystable Fano varieties,” Invent. Math., to appear.

许晨阳教授曾做客“墨子沙龙”，分享他的数学研究之路。以下是报告视频和演讲内容。

许晨阳：我很荣幸来到墨子沙龙，我讲座的题目叫代数几何——我的数学之路，因为当时墨子沙龙跟我说代数几何比较抽象，要做科普的话，可能讲一点更具体的东西更好。我其实自己也有这个感觉，我想来的很多是小学生、中学生，甚至可能刚刚上大学的大学生，如果讲数学理论，你可能不是一下子能知道我在干什么，但是我如果把我从事数学研究过程中的一些感受、一些认识跟大家分享一下的话，可能对大家会有一些帮助或者启发。

►保罗·哈尔莫斯

这个人可能大家都没有听说过，除非你是做数学研究的人，他当然是一个不错的数学家，但他并不是一个特别有名气的数学家，我上大学的时候读过他的一本书，叫《我要做数学家》，他讲了一个普通的数学家是怎么来面对工作的，我的题目叫我的数学之路，但我不是说我自己是一个多么伟大的数学家，我就想说作为一个普通的数学家，我们是怎么去面对工作，去选择数学之路的。

因为在座的大家可能都是比较喜欢数学的，可能你们都听说过高斯、黎曼、牛顿这些伟大数学家的故事，他们这些人都是数学史上的传奇英雄，你希望成为他们当然是一个很正常的想法，但我想最后能成为他们这样数学英雄的人真的是上帝的天选之子，一般的人可能没有达到这样的天赋。但即使像哈尔莫斯，像我这样的，我们这样一些普通数学家，我们自己也很喜欢我们的工作。

起点

我讲一下我是怎么走上数学科研之路的，我大概是1999年的时候参加国家集训队，保送进北大数学系。我现在回想起来，上大学以前，上中学，包括我做数学竞赛的时候，其实对现代数学到底是什么不太懂，没什么概念，我大概是在进集训队之后，因为能保送北大了，在不需要参加高考的那一年，我找了一些数学分析、线性代数这种大学生的入门教材自己来读一读，从那个时候我才认识到什么是所谓的大学数学、现代数学。现在有很多中学生同学，你们可能已经学了一些知识，但是你会看到你们现在学的数学，现在整个中学数学只是数学里面非常非常小的一个角落，其实真正从事现代数学的研究，我们所思考的那些数学问题，跟现在大家学的中学数学完全是不同的两回事情，这是我从上大学之后才知道的。

大学本科的时候我们学了哪些课呢？我们学了数学分析，像微积分、函数论，然后我们也学了很多代数，我这里写的只是数学中的一些你们上大学以前可能没有听说过的科目，比如说我们学了抽象代数，也学了群、环、域、伽罗华理论，大家可能听说过这些名词，但是我们上大学的时候专门学这些东西，然后我们也学了一些几何和拓扑，大家可能听说过几何，但拓扑可能不大见得听说过，然后我们也学过流形，这是现在几何和拓扑研究的主要对象，一般叫流形，如果大家没有学过大学数学的话可能都没有听说过这个词。

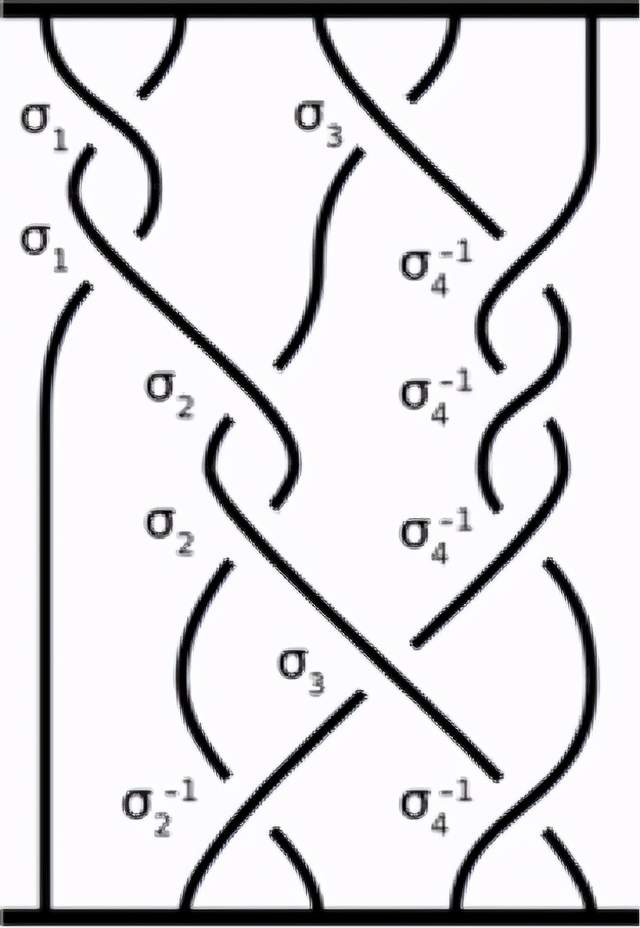
我这里画的图（指的是上面这个图）跟量子纠缠可能也有一点关系，这个是所谓的变群，这里面既有一点拓扑的概念，也有一点代数的概念，这个“变”字就是这里面的拓扑，“纠缠”实际上跟它具体（是什么）没关系，它主要是一个纠缠的关系，这种东西就叫拓扑。但是所有的纠缠形成了一种群的结构，当然我不会讲什么是群的结构，但是它里面有一个代数结构。

像这些东西，当时我上大学的时候印象很深，我刚刚开始看这个东西的时候就特别兴奋、特别激动，因为我觉得这个跟以前学的数学是完全不一样的事情，所以从那个时候我下定决心想要从事数学研究，但是我也不知道我能不能留得下来，因为你想做一份工作，并不是说你想做就一定能做得到的，只是说如果我能的话我尽量尝试去做数学研究。我上大学本科没多久，我想如果我能继续从事数学研究，我会把这个作为自己的职业。

这里引用一句很有名的赫尔曼·外尔的话，（上面提到的这些数学很多部分大概是21世纪初开始的，现在中学数学，如果你没有学到微积分的话，你学的数学基本上是一千年以前的数学，如果你学过一点的微积分的话，你大概学过一点三百年以前的数学，上面提到的这些大概是在一百到两百年以前的数学。）赫尔曼·外尔是20世纪初的一个非常伟大的数学家，他说，拓扑这个天使和代数这个魔鬼，这两种东西有非常不一样的数学研究味道，他们为了争夺每一个数学领域的灵魂而斗争。换句话说，简单翻译成中文是什么意思呢？就是说我要做代数研究还是做拓扑研究，我得想一想，大概就是这个意思。

代数的起源

我们现在来看代数，我想大家都解过二次方程，一元二次方程是可以求解的，你可能也听说过三次方程或者四次方程都有求根公式，但你可能也听说过五次方程以上是没有求根公式的，第一个严格证明这件事情的是Galois，而且Galois不仅证明了五次方程没有求根公式，而且他给出了一个原因，这个跟一些群有关系，就叫伽罗华理论，当然这个我不具体讲。

我想说的是我们研究这样的方程，这是一个很自然的事情，如果大家喜欢数学的话，你可能都问过自己这回事，你初中学一元二次方程或者小学学一元二次方程的时候，可能问过自己，为什么我们只做二次，当然三次四次你去书上找是可以找到这个求根公式的，到五次以上就做不到了。这个我以前上中学的时候就觉得这个事情很神奇，为什么五次以上没有求根公式，这个到我大二的时候学过伽罗华理论之后，终于明白这个是为什么。

所谓没有求根公式，指的是我没有一个公式把这个a1到a5写进去之后，把这个解给描述出来。但如果我把a1到a5都换成复数，很多人学过复数，代数基本定理就说这里面总是有一个解的，好象这两句话听上去有点矛盾，我第一个说没有求根公式，第二个我说有一个解，但是这个不矛盾，为什么呢？因为这个解只是没法通过一个求根公式表示出来，但是这个解本身是存在的。就是说一个东西存在跟能不能用一个公式写出来，这当然是两件不一样的事情。

我这里是一元多项式，任何一个多项式只有一个变元，不管次数多高，系数多复杂，只要是复数，它就一定有复数解，这也是代数。解方程，我为什么只解一元的，我们可以解多元的方程，我想大家可能都学过二元一次方程，你如果上大学的话知道解线性方程，不管有多少个元，我都可以用矩阵去解。我以前学数学的时候就会问自己，如果我们现在有很多个方程，这个次数不是一次的，怎么解呢，这也是很自然的代数问题，代数的起源就是说我们想去解这样的方程。

现在我这里写了一个方程，X二次方+X+1=Y三次方-Y，我说这方程一定是没有整数解的，有人知道为什么吗？这个方程没有整数解，它的原因很简单，因为右边一定是个偶数，左边一定是个奇数，X不管是什么，X二次方和X奇偶是相同的，所以我加1之后，它一定变成一个奇数，右边Y的三次方跟Y的奇偶性一定一样的，所以右边是个偶数。所以这个方程在整数上是没有解的，但你现在看，我不光是在整数上解，我想在复数上解，怎么办呢？我这个方程带有很多复数解的，因为我把Y任何一个复数放进去之后，我这边都可以找到相应的X，而且一般还有2个X，所以这个方程有很多复数的解。

我们现在考虑这样一个多项式，我这样写可能稍微有点抽象，如果回到前面的话，这里其实是两个变元的方程，这个方程次数到3，我就可以考虑所有这两个变元的方程x、y。你如果不是一个数学系的本科生的话，可能很少有这样的机会去想怎么解这样的方程，这个方程首先我们知道有很多解，因为我只要把y代入一个复数进去，这里Pi，j是某些复数，这就变成一个关于x的方程，相应的我就可以把x解出来，所以说这里是有很多解的。

但是我们并不满足于知道有很多解，我们想知道这个解到底长什么样，我们想知道这个解是无穷的，因为对任何一个y我这里都可以取不同的x，所以这里无穷多个解是没问题的。那我们想说怎么去研究这无穷多个解呢？我们的办法就是说我们把所有的解想象成一个几何的图形，最简单的情况就是这个，但是如果（i和j）加起来的次数等于1的时候，这个没什么好解的，因为如果是1的话，这里x只能是，就是a×x+b×y=c这样的形式，当然这是个线性方程，这个当然没什么好解的。

下一个目标，比如说n=2的时候，什么叫n=2的方程呢？最典型的例子就是x平方+y平方等于1，但是你现在要记住我们现在解不是在实数上解的，我们是在复数上解这个方程，所以你如果x平方+y平方等于1的话，在实数上我们当然知道它是一个元，但是如果在复数上解是什么样子？复数上解大概长这样，长成像球一样的一个解，这个当然不是那么容易看懂，如果你下来问我，我可以现场给你解释这个东西为什么是一个圆。

但是更复杂的，如果n等于3的时候，它就长成一个球一样的形状。如果n大于3的时候，它就长成这样，这个是非欧几何。当然很多喜欢数学的同学可能听说过这个词，非欧几何。人们研究所谓非欧几何好象只是数学家造出来的，但实际上并不是这样，它出现在非常多的一些自然情况里面。当这个n大于3的时候，比如我们现在一个解的空间，这个就是非欧几何。

以前在中学的时代，把x和y找出来这叫解方程。但是我们上大学的时候，这个解很多时候有无穷多个，我们怎么去理解这个解，我们想办法把它想象成一些几何的图形来理解，这就是我大概从事研究的代数几何，这个我后面会讲的更多。

我前面说了这个叫代数几何，其实是我上大学三年级的时候发现有这么一个学科，我当时特别喜欢代数几何的一个原因是，它把好多的数学统一在一块了，首先它这里面有一些分析，因为你想我解这个方程，我可以研究上面的这些函数，研究这种函数我们就叫分析，然后这上面也有一些代数，它有一些环和域的结构，比如它所有的这些函数构成一个环，如果你允许，还可以把这个函数相除，这就叫一个域。这上面还有更深刻的，如果你没有学过数学可能不太知道，上面有一个线丛和曲率的结构。前面这个图形我们都看到了，这些东西是怎么弯曲的，这个叫曲率，我后面会稍微花更多一点时间来讲。

我上大学的时候发现，原来我们以前学的数学，分析叫分析，代数叫代数，几何叫几何，但实际上它们是完全可以统一在一个学科里面，这个学科就是我从事研究的代数几何。代数几何实际上起源于阿贝尔、雅可比和高斯他们研究椭圆积分的时候，我不知道大家有多少人学过微积分，如果学微积分的话你就知道，我如果要积一个函数，是积分这个1除以根号x平方+1，这个函数我总是可以积的，这个是我们可以写成初等函数的，如果你学过微积分的话就知道这个应该怎么做，你去做所谓的欧拉变换，这是最初等的模型。

为什么我只开x平方呢，我为什么不开x三次方呢，我现在就想积分，我想积什么样的分呢？我积分积的是1除以根号x的三次方+1，这个我相信大家做数学分析的习题从来没有遇到过，因为这种积分是没法写成一个初等函数的。原因在于如果我把这个根号三次方+1开根，写成这个y的话，那么我积的这个方程是y的平方等于x的三次方+1，这个如果在我们前面画的那个图里面的话，就进入到n等于3的这个序列了。n等于3这个序列我们记得是长成这样的，这个就和我们通常积分的空间是不一样的，所以这就是大家开始说我们研究这样的积分，不应该直接去研究这个东西是怎么积，而去研究它这个积的空间是怎么样的，这就是代数几何的起源。

所以代数几何的起源，实际上就是我们去研究一些函数，或者去研究一些积分，研究一些解方程，我们需要把背后在搞什么样的几何给弄清楚。几何有比较简单的时候，像这种几何就是比较简单的时候，在这种情况下，往往你想做的不管是解方程的问题，还是积分的问题，都有一些简单的做法。但是这个时候当然是比较复杂的时候，当然这个更复杂了，这个就是说你得有一些数学的素养之后你才能理解这里面的区别是什么。

所以我大概就是在这个时候，开始对代数几何有很大兴趣，实际上我当年刚刚进入本科时，北大当时有一个项目叫本科生科研，我一开始做本科生科研的时候做的并不是代数几何这方面的本科生研究，我后来大概花了一点时间之后，很快发现实际上我最感兴趣的学科是代数几何，所以我大概在我上大学第三年左右就决定想要从事代数几何研究。代数几何这个东西，我前面写了具体的一些例子，包括阿贝尔、雅可比研究椭圆积分，阿贝尔和雅可比大概是两百年以前左右的人。

代数几何在上个世纪的前半叶，基本上是数学里面比较重要的一个学科，当时数学里面有很多很多重要的学科，比如说现在我们知道明年要举办世界数学家大会，数学一共分成了19个不同的学科，这个里面你如果把应用数学拿掉，只看纯数学的话还有十一二个学科，数学起码可以分成十一二个大的分支，代数几何在当时可能只是其中一支。

数学家

上个世纪60年代的时候有一个叫Grothendieck的数学家，我个人认为他是上个世纪最伟大的数学家，而且没有之一，他就是上个世纪最伟大的数学家。他当时做了一些事情，他把很多不同领域的学科研究都纳入到代数几何这个框架之下，就是说很多以前不知道跟代数几何有联系的一些学科，通过Grothendieck的工作之后，大家发现都跟代数几何有关系，你都可以用比较相似、统一的思维方式去思考，从那个时候开始，代数几何在数学里面的重要性就变得比以前更加重要了。

延伸阅读：数学怪才格罗滕迪克

很多人可能没有听说过这个人，即使我把他称之为20世纪最伟大的数学家，可能听说过他的人非常少，这个人是非常传奇的一个人，他的父亲是十月革命时期的一个革命分子，但可能并不是列宁派的革命分子，所以后来十月革命之后他们家就移居到德国，他是28年出生的，但他其实是一个犹太人，你就可以想象在1940年左右的时候他的一些人生经历。

当时他母亲带着他从德国，他们作为难民走到法国去，而且他小时候生活在法国的一个专门的犹太人的难民营当中。所以Grothendieck一辈子没有国籍，他后来去全世界进行数学讨论的时候拿的护照是一个无国籍护照，这个可能有很少人拿到，但是他拿的是无国籍护照。他大概在50年代中期，27、28岁的时候开始做代数几何研究，之前他其实做的不是代数几何，他大概做到1970年，做了大概12、13年，他在这12年当中写了上万种代数几何规律，就是这些工作把整个代数几何重新掀起了一场革命。

有人评价他，说他是在波澜不惊的地方建起了万丈高楼，就是说他在很多地方，一开始大家并不觉得这个里面有一些数学理论，他就在里面找出新的数学理论出来。

我之所以认为他是最伟大的一个数学家，是因为他做数学的方式是前无古人的，以前大家做数学问题，可能就是说我们去解决一个问题，这里有一个问题我去把这个问题解决了，那里有一个问题我去把那个问题解决了，他说不，他说我们做数学不应该去解决问题，应该去发展理论，他说我们把理论发展完了，理论成熟了，问题就能自然而然的水到渠成的可以解决，所以他从来没有把解决一个问题作为他做数学的主要目的，他的这种思维方式我想在以前的数学家里面可能是绝无仅有的。

我想说做数学要跟Grothendieck一样与众不同，真的是需要天赋。但我不是这样的人，我觉得即使你作为一个普通的数学家，你也可以有自己的生活方式，然后也可以有自己一份很好的职业，这个我会接着往下谈。

回到这个Grothendieck，我觉得他的思维方式跟正常人不太一样，他七几年之后做了一件什么事呢？他七几年之后就退出数学界了，他跑到一个山上去隐居，隐居了大概三四十年，就是他完全是一个人生活在房间里面，大概在2014年的时候大家发现他去世了。所以他是一个非常传奇的人，大多数数学家不是这样的人，大多数数学家是生活在大学里面做教授，有小孩有老婆，或者是有先生，过的跟普通人是一样的生活，他当然是一个非常不一样的人。

你如果学过代数几何就知道这本书，这本书是很多人学习的一个经典的教材，我当年花了一年的时间把这本书从头看到尾，这本书上面有很多习题，我花了很多功夫，一个一个习题去做这些。你学数学当然是要花很大功夫的，我印象中我当时做这本书的习题的时候，走在路上我也在想，我坐公共汽车都在想这个上面的问题，这个确实要花很大功夫。但是另外一方面，这个确实是你自己很喜欢做的事情你才会花这么大功夫，这个并不是说有人逼着我去干什么，真的是我自己觉得这是一个挺有意思的事，我才愿意去做。

浅谈代数几何

现在回到我从事的代数几何研究，代数几何是什么呢？代数几何说白了就是我前面说的，我有这些方程组的解，这个解它因为是无穷的，所以形成一个几何空间，然后我希望从几何的角度去研究这些方程组的解，这个叫代数几何。

我这里面写了几个方程，这些方程比较复杂，大家以前可能没有想过这么复杂的方程，这个里面有四个变元，是三次，我就把这些东西循环地解。这个解的方程，它的图像大概长的像这样（上图左），但实际上这个图只是一个非常近似的图，为什么呢？因为这个东西如果在复数上解的话，实际上是一个曲面，复的曲面，你有一个复数，你如果学过复数的话，会知道复数对应着一个平面，所以复数一个维度通常对应我们想的两个维数，所以如果讲复曲面的话，它实际上是复数上的二维，那么就应该对应一个四维的东西，所以这个你其实在脑子里面很难想象这是一个四维的东西。

我现在要说的是，如果画一个二维的近似图，大家看长成这样（上图右）。这个就更复杂了，这个叫Calabi-丘三维簇，这个实际上是一个六维的，复的三维，所以是实的六维的东西。你看这个图当然是非常漂亮的，但是这个其实只是二维的一个截影，关于这个六维的截影。所以我们做这个代数几何研究的时候，并不是像你解这个解析几何一样，我把这个图画出来，我去看这个图是怎么研究的。你看显然我是没法对着这种图去研究怎么去长这个代数结构的，所以你得经过一些很系统的训练，学习怎么去思考一个几何对象。

其实我们一般把空间分成三种，正的弯曲、负的弯曲和平坦的，这两个空间当中一个是正的弯曲，一个是平坦的，你现在可能看不出任何东西是平坦的，但是这个东西其实是平坦的。如果你看过一点科普，你可能听说过弦论，我是一点不懂弦论，弦论当然是很玄了，弦论里面有一个观点是说我们生活在四维时空，实际上不是四维，是十维的。

我们现在考虑这个十维的时空，我们通常只能看到四维，剩下六维到哪里去了呢？他说剩下的六维坍缩在一个非常小的尺度里面，所以我们是看不见的。但是根据弦论，这个六维不是一个随便的六维时空，它是一个像Calabi-丘三维簇一样的东西。所以这个东西虽然看上去非常复杂，但是它确实有可能跟我们的现实生活是相关的，当然前提是你相信弦论。你如果不相信弦论的话，当然你也可以把它完全作为一个数学对象来研究，这个里面就说它实际上是平坦的。

我前面说研究代数几何，为什么我们要用几何的办法来研究代数，阿蒂亚是一个非常伟大的数学家，他说过一句话，他说代数实际上是魔鬼给数学家的一个东西，他说魔鬼是这么说的，魔鬼说我给你一个非常强有力的工具，这个工具可以回答你任何的一个问题，但是作为交换，你要把你的灵魂给我，他说这个灵魂是什么呢？灵魂就是你要放弃几何，然后这样的话你就可以有非常有用、非常有效的工具。

这个话是什么意思呢？代数是一个非常有效，而且非常干净、非常整洁的东西，你在代数上做一些符号性操作的话只要不犯错，每一步都是非常严格的。几何里面有一些人的直觉在里面，阿蒂亚就说你拿代数方法来研究几何，你可能会失去你的几何直觉，但是你得到这个代数就是非常严格的。所以代数几何，你希望两个东西都要有，我既有几何上的一些直觉，可以拿来帮我研究这件事情，同时我也获得了代数上非常有利的工具。代数几何基本上就是说我希望既在有代数这个强有力工具的同时，仍然没有失去我的几何直觉，这就是代数几何研究的一个出发点。

百万美元的问题

如果大家没有接触过现代数学的话，你可能对现代数学是什么样子都没有观念，其实现代数学里面有非常非常多没有解决的问题，其中有一个科学研究所他们当时就找了一些数学家专门列了七个千禧年的问题，这个是在2000年的时候所以叫千禧年问题，每个问题你解出来他给你一百万美金，所以这个又被称为百万美元的问题。这七个问题里面包含了数学中很多不同的方向，但是这些方向并不是数学里面所有的方向，像这个庞加莱猜想，这七个里面现在已经有一个被解决了，就是所谓的庞加莱猜想，但这也是仅有的一个被解决的，剩下六个现在大家都不知道该怎么解决。

我们不同的数学家对什么时候能解决这个问题可能有不同的看法，希尔伯特也在1901年的时候说过类似的话，当时大家问了他三个问题，一个是超越数问题，一个是费马大定理，一个是黎曼假设。他当时说黎曼假设应该在我的有生之年能够看到它的解决，费马大定理（的解决）也许你们在座的人有生之年能看到，他说这个超越数问题现在我还没有任何办法。但实际上超越数问题在他的有生之年就已经被解决，费马大定理也是在上个世纪的95年被解决了，但是黎曼猜想过了一百年还被认为是最重要的问题之一，几乎在过去一百年没有像样的进展。

所以我们不同的人对数学发展会有不同的看法，不管怎么样，我这里只列了七个问题，但是数学其实还有很多其他重要的问题，可能因为他们当时只投了七百万美金，所以他们只列了这七个问题，但如果我要说现在一个问题我给五十万美金，我可以找十四个问题出来，这也是完全没有问题的。

七个问题属于不同的领域，第一个跟代数几何最接近，叫霍其猜想，我现在没法用简单的语言来描述，因为要明白霍其猜想在讲什么这个已经需要很多代数几何的知识。

第二个是BSD猜想，它是一个等式，有一边是用代数几何来描述，一边是数论的描述，它说这两边是相等的，这个被称为BSD猜想。

第三个就是大家说的黎曼假设，黎曼假设本来是研究素数分布的，所以它其实是关于数论的一个问题。

大家都知道现在算法很流行，理论计算里面有一个最基本的问题，P vs NP，就是P是不是等于NP，一般大家相信P不等于NP，但是现在还没有严格的证明。

这个是数学物理，杨-米尔斯理论是一个物理理论，但它能在数学上严格化，这个不管对数学还是对物理，都是一个很基本的事情，所以这个大家也不知道。

然后微分方程，是纳卫-斯托克斯方程，什么叫纳卫-斯托克斯方程呢？它的研究对象是湍流，你如果走过一条河，会看到里面有很多漩涡，描绘这个旋涡的方程叫湍流方程，你现在有微分方程了，想去解它，如果你不是一个数学家你怎么解这个方程呢，我就把这个输进去，然后计算机模拟，就模拟出很多数字解。但你如果是一个纯粹的数学家，你就想我们其实更希望从理论上来理解这个解，我们希望这个解一定是光滑的，这个就是说所谓的纳卫-斯托克斯方程，这个也是不知道的。

最后一个是庞加莱猜想，这是一个拓扑问题，它描述的是什么呢？它描述的就是我们生活的三维空间，我前面画了一个图，是一个球，一个像轮胎一样的东西，还有一个非欧几何（PPT第六页），这个是关于曲面，一共只有三种几何。庞加莱猜想其实是研究三维的，这个三维就像曲面一样，它一共只有八种几何，然后庞加莱说我们怎么把这八种几何刻画出来，庞加莱猜想就是说刻画这个球，这个当时是被佩雷尔曼解决了，而且佩雷尔曼实际上把整个三维的八种几何刻画全部解决了。

我想说一点，这个庞加莱猜想其实是关于长什么样子的问题，这是一个拓扑问题，它的解决里面其实用的最多的是分析，用的最多的是几何，所以说你解决这六个问题完全有可能是依赖于一个新领域的技术，这个在数学里面是非常常见的。就是说真正这种大的问题，之所以大，这个问题没解决出来，很可能是因为我们没有找到别的什么领域的技术去研究这个问题，这个在数学里每次发生都意味着数学的一次革命。就是说我们发现两个之间毫无联系的领域它们之间可以联系起来，比如说BSD猜想，一半是代数几何，一半是数论，这两个本来看似毫无联系，通过这么一个猜想把它联系起来，很有可能这六个问题的解决需要的技术。要么完全是新的领域，要么可能都还没有产生，这也是完全有可能的。你知道这个费尔马猜想提出的是一六几几年，350年以前，那个时候的人你不管有多聪明，你都没法解决费尔马猜想，起码没法用最后的那种办法解决费尔马猜想，因为最后怀尔斯的解决是建立三百多年数学一步一步发展之上的。

所以数学发展有可能是这样的过程，实际上有一个整个理论在往前运行，所以可能跟很多人想象的不一样，你可能不知道现代数学到底发展有多快。实际上我想说现代数学其实发展非常快。比如说我前面说的费马大定理，这个350年的问题，在20年前被解决了。

像这个庞加莱猜想，被解决的时候已经提出来一百年了，也被解决了，还是有一些非常基本的问题，在我们过去十几年二十年的时候被解决了。像这个费马大定理，我记得解决的时候是我上初中的时候，所以我上小学的时候费马大定理还是一个猜想，当我上初中的时候它已经是一个定理了。当我上大学本科的时候，庞加莱猜想还是一个猜想，当我读博士的时候它已经是一个定理了。所以说你真正能看到，这是我自己喜欢数学二三十年来看到有这些非常伟大的问题被解决掉，你如果真的从事数学研究，很多时候能看到理论一点一点往前进。

我想说作为一个普通数学家，我觉得这个对我来讲，也是一个让我非常激动、非常振奋人心的过程，就是说我真的是能看到这个理论一点一点往前发展。就像大家看到这个科技在发展一样，看到这个世界一点一点被科技改变，但是数学理论发展没有那么具体，但是你作为一个数学家，你其实能看到这个理论真的是在往前发展。

数学是年轻人的学科

现在讲到我本科的时候，后来我去读博士，我04年的时候去了普林斯顿读博士，这是普林斯顿著名的校门口。我当时出国的时候是在北大，因为我一起读了本科和硕士，所以我大概04年的时候想出去兜一圈，因为在我读书那会儿，代数几何在中国实际上不是很多人从事研究的项目。比如说在北大，实际上从事代数几何研究的老师是非常少的，所以我当时就想去，中国以前很多人做的是微分几何这个领域。

除了自己比较喜欢代数几何以外，还有一个小的因素是我想去从事以前中国人做的比较少的领域，自己去尝试一下。当然普林斯顿是一个代数几何的中心。你如果看过一部电影《美丽心灵》的话，会知道纳什就在普林斯顿，你看《美丽心灵》里面出现的普林斯顿校园都是长成这样的，包括我前面这张照片，校园看上去都很漂亮，但是只有数学系是非常不一样的一栋楼，你如果到普林斯顿校园去看，真的大概只有数学系大楼长成这样，大部分楼大概都是这样子，所以数学系当然有一种卓尔不群的风姿。

你如果去普林斯顿的话，我印象最深的就是在普林斯顿的路上遇到的任何一个教授都是当今科学界的巨擎，你如果去数学系，你遇到最有名的人是谁呢？大概就是怀尔斯，他就是解决了费马大定理的人，他花了七八年的时间来研究费马大定理，最后真的是把它给解决了。你可以到网上去找他的一些访谈，我觉得他整个解决方法，他人生的过程，他从小就开始喜欢数学，这都是很有意思的一些访谈。

我前段时间看他得诺贝尔奖的访谈，他里面提到他从小就很喜欢数论，但是不是那么喜欢几何，我跟他比我就相反，我更喜欢几何，不是那么喜欢数论。

所以我想每个人其实对数学的喜好还是有不一样的，之前有一句话叫世界之美来自于参差不齐，我想数学也是这样，数学里面有很多不同的学科，可能你找到你自己最喜欢的学科，这本身就是一件很有意思的事情。

我当时就想从事代数几何研究，当时在普林斯顿有两位专门从事代数几何研究的教授，一位是Kollar，一位是Pandharipande。Kollar在我去普林斯顿那年，2004年的时候他是35岁，你可能会想35岁在普林斯顿做教授，这个算是年轻有为了，但实际上数学跟其他学科有点不一样，尤其是跟实验学科有点不一样，就是数学里面的人其实很多成名是非常早的。

我的理解是你要从事实验这种学科，你可能需要大量的经费，这个需要你在社会上积累了一定的的信誉，大家才相信你，愿意把这么大笔的经费交给你来管，让你来做这个实验。但是数学还是一件比较个人的事情，所以你很有可能来自于一个大家都不知道的地方，但是突然就解决了一个问题，因为很多时候你不需要别人太多帮助，有的时候大家说数学是一个年轻人的学科，这个其实还是有道理的。

你如果看普林斯顿、哈佛这些学校的历史，你看他们校史上最年轻的教授都是数学教授，比如说在普林斯顿，我当时在普林斯顿的时候有另外一个教授，他是20岁在普林斯顿毕业，24岁已经是普林斯顿的教授了，他22岁的时候是芝加哥（大学）的教授。我不知道这里多少同学已经超过22岁了，反正我是远远超过了，他22岁就已经在芝加哥大学做教授了，所以数学是一个年轻人可以独立地做出很多贡献的一个学科。

我最后选择了Kollar作为我的博士生导师，因为他们两个在代数几何方面的研究也有一些区别，后来我更喜欢高维双有理几何，所以我就选择Kollar做我博士导师。

Kollar这个人是比较古典的人，现在大家都喜欢写论文，大家看论文发表在影响因子多少的杂志上，好象这是评判一个大学老师做的好不好最主要的因素。但是你如果回到一百年前看的话，数学并不是这样子，那个时候数学真的有好的理论的人都是写书，他们那个时候研究的节奏可能比我们要慢，但是他们往往把一个理论整理的比较成型之后，写成一本很厚的书，然后对整个理论有一个非常完整的研究之后，再来把他的研究内容总结出来。

Kollar就有这样一种比较古典的气质，他写了很多书，这里面每一本书都是Kollar或者Kollar跟别人合作的，这是我当时准备这个PPT的时候，我就把我办公室里面的书照了一遍，那些书都在我办公室里面，所以我做这张PPT的时候花了很多时间。

当然我也没有每一本都看，你做博士研究的时候跟以前中学学习（不一样），你中学学习别人告诉你该干什么你就干什么，所以你所有的（知识）都是沿着一条线往下学的，这还是一个线性的学习。到研究的时候，很多时候没有人告诉你该干什么，所以你学习的过程跟做研究的过程是一个同时的过程。

比如说，今天我学了这个书的第三章，因为我研究问题的时候需要这个东西，然后我明天研究这个问题需要这个书的第五章，我就学这个书的第五章，所以到后来你学习跟研究的过程就是一个同时的过程。到今天我还在学习，我经常还要去学习别人的论文，或者有的时候看书学习新的理论，所以我觉得（这是）作为数学家另外一个很好的一点，有一句话叫做活到老学到老，但可能有很多职业实际上过了某一个阶段之后，你从事的这种学习不再是知识理论的学习，你可能要学习一些别的，但不再是知识理论学习了。但是数学这个职业有一个好处，就是说这一辈子你可能都还会从事一些知识理论的学习。

大家来听这个讲座的人都是比较喜欢学习的人，你知道学习这个过程，一辈子都有目的、有动力的学习，这就是一个很好的体验。另一方面你可以做研究，可以从事一些创造性的活动，这当然是另外一个更好的体验。我在读博士的时候，已经下定决心跟Kollar从事双有理几何的研究。

双有理

经常有人会问我什么叫双有理，这个词你听上去挺怪的，这是一个中国人翻译的，（英文是）biration，双有理研究的是什么几何对象呢？就是一个东西到另外一个东西，两个几何空间，它们两个沿着一个比较低一维的东西不太一样，但是除了这个低一维的东西，剩下的东西它们都是完全一样的，这两个东西就叫双有理等价，双有理几何就是说我们在这个等价的意义下来研究几何。

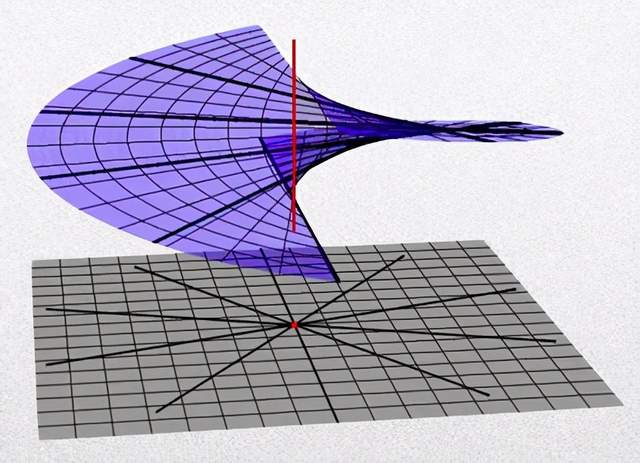
你看这个图，我现在取每一条线，然后我把这个线的切方向拿出来，你本来是一个平面的，但我现在不把它想象成一个平面，我把它想象成是过一个点的所有的不同的射线并在一块，然后我把这些射线全部打开，就变成了上面这个图。所以说这个东西跟这个图，它本质上的区别就是我把这条线给压缩成了这个点，除了这个线以外、这个点以外，它们都是一样的，这个就叫双有理等价。

我们的目的是什么呢？我们的目的就是说我给你一个空间，希望通过双有理几何把它分解成三种基本的类型，要么是正的弯曲的，要么是负的弯曲的，要么是平坦的。比如说什么叫弯曲，这个就是三个弯曲的空间，这是正弯曲的，为什么呢？因为你在这个上面做一个三角形的话，你会发现它的内角和是大于180度，这个就叫正弯曲的空间。

这个东西你想象当中好象不太是平坦的，它之所以不是平坦的，是因为你没有正确的去看它，我应该怎么正确的去看它呢？我先拿一张纸出来，我把这个纸上下给粘起来，就变成了像桶一样的东西，我再把这一头一尾粘起来，你在三维空间没法想象怎么把它粘起来，但是你可以想象在一个抽象的世界里面把它给粘起来，这样的话我就把一个平坦的纸给粘成了这样的东西。

纸当然是平坦的，所以我粘成这个东西也是平坦的，所以如果我正确去想象它的话，这个世界应该是平坦的，而且实际上你把这个三角形在这上面做的话，你就会发现它的内角和真的就是180度。这个图，你现在可以看出，它的内角和总是小于180度，所以它是负的弯曲。就是说这种几何，就是我们把这个几何总是分解成这三种基本的类型，正弯曲、平坦或者负弯曲。

怎么来描述这个弯曲呢？不同的人有不同的办法，最早描述弯曲的办法是所谓的微分几何学家，最早是高斯在曲面的时候研究出来的，然后黎曼在所有的维数（研究）。

关于他们俩，我想各讲一个故事。黎曼研究微分几何，刚发现的时候它当然只是一个数学理论，但是到了1910年的时候爱因斯坦发现他做广义相对论的话，需要一些跟以前不一样的数学结构，他就去问他数学家朋友，我相信他应该是问希腊数学家卡拉塞奥多里斯，卡拉塞奥多里斯就告诉他，他需要的数学几何空间的理论，实际上已经在五六十年前被黎曼（建立起来了），黎曼建立黎曼几何大概一八五几年的时候。

当时黎曼建立这个数学理论的时候，只是说他要对这个世界有一个更深刻的认识，但是当时并没有物理学的东西来支撑他，但现在我们知道广义相对论是支撑黎曼几何的，确实是有一个现实性的依托的。

高斯的故事我也讲一下，我想大家都听说过高斯的故事，高斯的故事我想大家第一次听说应该是从1加到100的时候，听过他可以把两边加起来，乘以100，除以2。我想说的高斯的故事就是这张照片，我们现在说大家多么尊重科学，但你看德国人是怎么尊重科学的，这是一张十马克的德国马克的照片，这个是在欧元以前德国的货币，德国人把他们的数学家印在了货币上，你想想我们的货币，这个尊重科学的程度还是不太一样的。

代数几何里面没有曲率的概念，微分几何需要在空间里研究它的度量，你要知道这两个点有多远，但是多远并不是一个代数几何的概念，因为代数没法研究两个点之间有多远。比如我现在有两个方程，我这个方程上面有两个点，我说它们之间有多远，这个东西在代数上是看不到的。

代数说我们没有局部的办法研究两个点多远，但是我们有整体的办法来研究，这个整体的办法就是所谓用拓扑来研究，拓扑这个学科是在数学学科里面出现相对比较晚一点的，拓扑作为一个学科被真正建立，大概就是在上个世纪初的时候，或者上上个世纪末的时候，庞加莱建立起来的。我们说代数几何没法描述这个距离，也没法去描述角度，但是我们可以整体地去把握这个空间到底是弯的还是正的。

怎么整体来看呢？实际上很简单，我们就用欧拉数来看，我要说这个空间是正弯曲的，我需要它的欧拉数，你知道欧拉数是什么？欧拉数就是，面的个数，加上它的顶点的个数，然后减去这个线的个数，但得做个三角剖分。这个我们知道它的欧拉数是2，这个的欧拉数是0，这个的欧拉数是-2。这个其实就是刚才那个负的曲面，我把它粘成这个样子，所以换句话说，我其实解这个方程，正弯曲的时候欧拉数是正的，平坦的时候欧拉数就是0，负弯曲的时候欧拉数就是负的。但是欧拉数实际上是可以通过代数几何来描述，因为这是一个整体的概念，这并不是说两个点距离有多远。这是一个整体的办法，因为拓扑其实是一个整体的东西，所以代数几何当中可以整体的来定义这个是正弯曲、零弯曲还是负弯曲。

这其实是一个非常深刻的概念，比如现在要解这个方程，我刚才说解复数方程有无数个解，一般在中学的话，你可能没有学过复数，那我现在解整数，但是整数还不能除，为了可以除我就先在有理数上解。我那个方程是x的i次方，乘以y的j次方，前面有一个系数是Pi,j。我如果想在有理数上解这个方程，Pi,j本身得是有理数，比如最简单的例子，我想解x的n次方+y的n次方=1，这个完全是个有理数方程。

这个是Faltings当年得菲尔兹奖的工作，他告诉我们说，如果是负弯曲的话，上面的解永远只有有理数，这就是一个很奇怪的事情，本来正负弯曲只跟空间长什么样子有关系，但他最后说空间的个数决定了在有理数上解的个数。换句话说，你本来是连续的几何，比如说这个空间是正、还是负，这是很连续的几何概念，然后有理数是很离散的东西，他告诉你这个连续的几何某种意义上决定了你这个离散的东西的概念。这当然是一个非常伟大的证明，以前被称为Modell猜想，Modell提了四五十年以后被Faltings在1984年左右解决。所以这三种空间，正的弯曲、负的弯曲、平的弯曲，它们有很多基本的不同，比如说，如果只是解有理数方程，它们解的个数表现出非常差异的性质。

双有理几何中，当然解的空间有可能非常复杂，但我希望把它分解成这三种基本的模块，要么是正的，要么是平坦的，要么是负的。分解的过程现在我们有一个算法，叫做极小模型纲领。数学里面一般叫纲领的东西代表两件事情，第一个是它可能还没有完全解决，还有一些猜想性的东西，所以它叫纲领。还有第二个，就是它可能是一个比较庞大的结构，里面可能有很多问题，放在一块才叫一个纲领。

双有理几何这一块就叫极小模型纲领，极小模型纲领是什么意思呢？就是说给你任何一个解的空间，希望通过一些手术，把它分解成三种模块，要么是正的，要么是负的，要么是零，这三种模块被称为极小模型。曲面的时候，就是十到四维的时候，大概是在一百年前，由意大利学派，特别是Enriques解决的，后来是小平邦彦，这是个日本数学家，他也做了很大贡献。

你如果去网上查，有一个关于这个小平邦彦的传记，不是很长，这个传记的题目叫《游里工夫独造微》，这句话翻译出来是什么意思呢？它是中国古代的一句古诗词，大概变了一个字，这句话是形容小平邦彦做数学的进度，原话翻译是，像流水般随意游玩，但在心底里凝神钻研，独自洞察真理之奥秘。

我觉得其实这是对做数学研究境界的一个非常好的描述，就是首先你得很自由，所谓流水般随意游玩，当然不是说叫你去玩，这个意思是你做数学的时候可以处于一种非常自由的状态，可以自己去选择想做什么样的研究，可以自由的去想象你应该从哪个角度去研究。但是第二句话是说心底里凝神钻研，是说你一定要聚精会神，把整个自己交给做数学研究这件事情。最后是独自洞察真理之奥妙，就是最后你真的发现了数学界里隐藏的一些事实，这就到了你发现数学真理的时候。我特别喜欢这句形容小平邦彦数学研究境界的话，我想这可能也是很多数学家想要追求的一个境界，你们可以到网上查这个传记，题目叫《游里工夫独造微》。

延伸阅读：

游里功夫独造微 | 游里工夫独造微——小平邦彦传（上）

游里功夫独造微 |