为什么围棋对人工智能很重要？

自人工智能诞生以来，让机器自动玩智力游戏并寻求战胜人类，就一直是人工智能领域追求的重要目标之一。因为智力游戏被公认为是智能的一种具体表现，而人工智能的终极目的就是用机器实现人类（部分）智能。人工智能正式诞生的元年，即1956年，阿瑟·萨缪尔(Arthur Samuel, 1901—1990)就编写一个程序下西洋跳棋战胜了他自己；1962年，这个程序击败了一个美国的西洋跳棋州冠军；1994年，一个新的西洋跳棋程序Chinook战胜了人类总冠军[3]。1997年，IBM开发的深蓝击败了国际象棋世界冠军卡斯帕罗夫，当时也引起了巨大轰动[4]。

图1阿瑟·萨缪尔

图片来源：google

图2被Chinook打败的人类冠军Marion Tinsley

图片来源：wikipedia

图3深蓝与卡斯帕罗夫对战现场

图片来源：google

为什么在已经证明了机器下西洋跳棋和国际象棋比所有人类都要厉害的情况下，还要做围棋？为什么围棋最受关注，而不是其他智力游戏，比如五子棋呢？这里最关键的原因在于围棋的复杂性。更确切来讲，围棋是所有大家熟知的智力游戏中，搜索空间最大的，所需要的计算量也是最大的。

简单估算一下，从棋盘状态来看，围棋棋盘是有19*19=361的格子，每个格子有3种可能性（黑、白、空），所以总共有3^361，将近5千万个状态；从下棋步骤角度来看，即使不算吃子和打劫，第n步有361-n种选择，所以至少有361!——超过10^200种可能性，比宇宙原子的总量还要多，也远比其他智力游戏（诸如国际象棋、五子棋等）的搜索空间大很多。所以，围棋被公认为这类问题中的皇冠，很难被人工智能解决。

图4 一个围棋棋盘状态

图片来源：google

AlphaGo  Zero的前世

AlphaGo Zero并不是石头里面蹦出来的孙悟空。在此之前，人工智能界做过很多努力，也总结出了很多有效的思路、经验和技术。用机器来玩智力游戏，首先的步骤是建模，即把这个游戏表示成一个机器可以处理的问题。同西洋跳棋和国际象棋一样，围棋可以被建模成一个搜索问题。更具体一点，下棋的步骤可以表示成一个搜索树，其中每个节点代表一个棋盘状态。根节点是空白棋盘，每个节点的子节点是在当前的棋盘下采取一个行动，即再多下一个棋子，而每一个叶子节点是一个下满了棋子的棋盘状态。而机器要做的事情，就是从当前节点中，尽量找到一条路径，到达能够使己方赢的一个叶子节点。

图5

图片来源：google

图6搜索树模型

图片来源：google

为了找到路径，人工智能传统的解决方案是“搜索”。所使用的技术包括经典的深度优先搜索、启发式搜索、剪枝等等。这个方案能解决很多简单智力游戏，如八皇后、数独等，但由于计算量太大，并不能解决复杂问题比如国际象棋和围棋。所以，只能退而求其次，在当前节点（即棋盘状态）中，找到一个最优或较优的子节点。因此，研究者们提出一个新的方案——“评价”。在这个方案里面，不再苛求搜索到一条最佳路径到达赢的叶子节点，而是对每一个节点，估算出一个最佳的子节点。也就是说，对每一个当前的棋盘状态，评价出最佳的下一步行动。

评价的对象主要有两种：一是棋盘状态的“策略”，即遇到当前状态，高手（包括人类和电脑）都是怎么下的，选择每一个子节点的概率分布如何。其输入是一个棋盘状态外加一个可选的行动，而其输出是在当前状态下选择该行动的概率；二是棋盘状态的“赢面估算”，即每个子节点赢的概率有多大。其输入是一个棋盘状态，而其输出是这个状态能赢的可能性。在理想的情况下，这两者应该是一致的，即选择概率高的子节点赢面就大，反之亦然。然而，实际上这两者往往有些差别。

评价的方法就五花八门了，启发式函数、贝叶斯、蒙特卡洛方法、深度学习等等，不一而足。这里简略介绍一下蒙特卡洛树搜索方法[5]。在AlphaGo  Zero中，该方法和深度学习至少同样重要。蒙特卡洛树搜索在每个节点上做很多次随机游戏。每次随机游戏随机选取一条到达叶子节点的路径，也就是每一步都随机落一个子。最后，该节点的赢面就可以被估算为这么多次随机游戏中赢的百分比。虽然简单，但蒙特卡洛树搜索方法却相当有效，一个基于该方法的围棋程序能够达到业余段位的水准，比大部分普通人强。

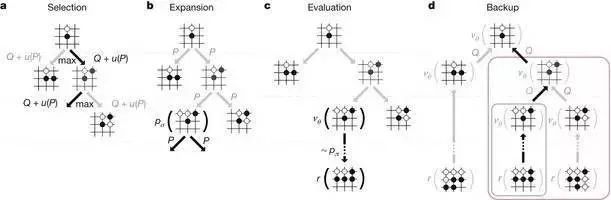
图7蒙特卡洛树搜索方法

图片来源：google

基于评价的方案对很多智力游戏都行之有效，包括西洋跳棋、五子棋、国际象棋等。事实上，这个方案也能完美解决5*5，7*7的围棋。然而，正如前面提到的，19*19的正规围棋搜索空间太大。所以，受限于计算能力，在AlphaGo Zero出来之前，基于评价的方案还无法摘取这个皇冠。大部分人都认为19*19围棋对现阶段人工智能技术来说，基本不可能被解决。

AlphaGo Zero的今生

然而，AlphaGo Zero横空出世，颠覆了人们的认知。2015年10月，AlphaGo 5:0击败了欧洲围棋冠军樊麾。2016年3月，AlphaGo 4:1击败了前世界冠军李世石。2017年5月，AlphaGo 3:0击败了世界排名第一的中国选手柯洁。在这段期间，一个AlphaGo的改版程序Master在各大围棋平台上以60:0不败战绩横扫各路围棋英豪。然而，更惊奇的是，2017年10月，AlphaGo自我创新，提出了一个新的变种AlphaGo Zero。该程序完全不依赖人类专家的对局，从零开始，使用强化学习的方法；仅用一台带有4个TPU的机器，40天下了两千九百万局棋；从中自我进化成了一个新的围棋界的“独孤求败”；100:0吊打李世石版本AlphaGo，89:11痛殴Master。至此，基本可以论断，在围棋领域，机器已经完胜人类了。

图8 AlphaGo与柯洁对战现场

图片来源：google

从技术角度来看，AlphaGo Zero继承并改进了之前的框架。AlphaGo Zero依然把围棋建模成一个搜索问题，依然采用基于评价的方案来做决策。其主要的学术贡献在于提出了一套新的估算评价函数的方法，更好地融合并改善了已有的两种重要的方法（即蒙特卡洛树搜索方法和基于深度学习的方法），从而达到了惊人的效果。

大致上来说，AlphaGo的评价方法分成四步[2]。第一，AlphaGo以大量人类专家对局为数据，采用有监督学习的方法学习了一个深度神经网络SL来估算策略；第二，在SL的基础上，AlphaGo和自己左右互博，采用强化学习的方法把这个策略神经网络改进成一个新的深度神经网络RL；第三，AlphaGo再在RL的基础上，还是和自己左右互博，还是采用强化学习的方法学习了另一个深度神经网络V来估算每个棋盘状态的赢面；第四，再使用基于蒙特卡洛树搜索方法的算法，巧妙加权融合了策略网络SL/RL和赢面估算网络V，来做最终的决策。

同AlphaGo相比，AlphaGo Zero作出了很多重要的调整[1]。简而言之，去掉了第一步，而把剩下的三步合并成为一步“基于蒙特卡洛树搜索的强化学习”。AlphaGo Zero把AlphaGo中间的策略网络SL/RL和赢面估算网络V合并成了一个深度神经网络，减少了评价方法的复杂程度。同时，AlphaGo Zero改进了蒙特卡洛树搜索方法，在每一步随机选取行动的时候，不再是完全随机，而是根据已经学习到的神经网络，尽量选取赢面大的行动。然后，强化学习又反过来使用了改进版本的蒙特卡洛树搜索方法得到的结果来调整自身参数。这样，蒙特卡洛树搜索和强化学习就很好地结合到了一起。

此外，由于去掉了AlphaGo中的第一步有监督学习，AlphaGo Zero完全不需要使用人类专家对局作为数据输入。从而，某种意义上，AlphaGo Zero可以被认为是完全从零开始学习，从“白丁”到“鸿儒”，所需要的只是对其输入围棋基本规则，这一点，对于当前机器学习和人工智能有非常重要的意义。

为了更好地弄明白这点，需要解释一下机器学习中有监督学习、强化学习和无监督学习的含义以及差别。

广义上来讲，所有的问题都可以表示成一个抽象函数，有着输入和输出。比如图像识别：输入是一张张图片，输出是不同的识别物体；句子的句法分析：输入是句子，输出是句法分析树；新闻分类：输入是新闻，输出是新闻之间的相似度；而下棋，输入是棋盘状态，输出是当前状态的最佳行动。机器学习的任务就是从数据中学出来这个函数，至少越来越近似这个函数。

其中，最核心的问题就是数据是长什么样的？在理想的情况下，我们期望这个数据是完整的<输入，输出>对，也就是说（近似）正确的输出在数据中被“标注”出来了。标注就是所谓的监督；而在这种情况下的学习，就是有监督学习。而在另外一种情况下，数据只包含输入，而不包含输出。也就是说完全没有标注，这种情况下的学习，就是无监督学习。

但还有一些情况介于这两者之间，其中包括强化学习。强化学习和无监督学习类似，数据中并不包含输出。但是，和无监督学习不同的是，强化学习中的数据也不只包含输入，它还包括了一个数据迭代运行多步之后的奖惩机制。比如踢足球，每一步的输入是当前状态，而输出是可能选择的行动，如传球、射门等。然而，很多情况并不能够直接给出在当前状态下最好的输出是什么。但是，一旦进球了，我们就能够给出一个奖惩机制。进球就是奖励，被进球就是惩罚。

又比如在下棋中，虽然每个棋盘状态下的最佳行动很难给出，但下完之后的输赢很容易判定。这就是奖惩机制，这就是一个典型的强化学习问题。注意，强化学习中的奖惩机制一般是在多步迭代后给出，如果只是一步的话，强化学习就变成了有监督学习。所以，从数据的角度来看，可以大致认为有监督学习就是一步奖惩的强化学习。

对于某个具体的问题，该用哪种学习呢？答案是，都可以用，取决于有什么样的数据。例如下围棋，原则上应该是一个强化学习问题，因为只有最后输赢的奖惩机制才是无异议的。但是，（人类和电脑）高手们在遇到某个棋盘状态时，会有自己的选择。这些选择虽然不一定是最佳的，但总归大体上都是很好的选择。所以，（人类和电脑）高手们的棋谱就提供了很多这样的<输入，输出>对（即<棋盘状态，选择>对）。这些，可以作为有监督学习的数据。

直观上，数据给的越好越多，那么学习的效果就应该越好。所以有监督学习应该比强化学习奏效，而强化学习应该比无监督学习奏效。这点在实际上也得到了验证。事实上，当前在商业领域的机器学习应用，包括语音识别、图像识别、句法分析、机器翻译等，绝大部分都采用的是有监督学习。然而，有监督学习需要用到的数据（即<输入，输出>对）从哪里来？输入好办，但是（近似）正确的输出却很难得到。为了得到正确的输出，往往需要人工来“标注”。机器学习在近十年内取得的巨大成功，离不开相当多在背后默默做标注的人。高质量大规模标注好的数据集，比如图像处理中的ImageNet [6]，自然语言处理中的Treebank [7]，极大地带动了机器学习的发展和突破。但是，标注往往极为耗时耗力耗财，很多时候只有大机构长期投入才能完成。为了解决“数据”来源的问题，人工智能界主要提出了两条思路。一条就是依靠机器某种方式自动生成和标注数据，如最近很流行的生成对抗网络。另一条就是考虑有监督学习之外的其他机器学习手段，比如强化学习。

图9 ImageNet

图片来源：google

AlphaGo Zero证明了后者是完全可行的，至少在机器下围棋这个领域。AlphaGo Zero甚至比AlphaGo还厉害，这是不是这意味着强化学习比有监督学习厉害呢？并不是。除了算法上的改进之外，AlphaGo所用到从高手棋谱中得到的数据，即<输入，输出>对（<棋盘状态，选择>对），并不一定是最优解。这是关于数据质量的问题。对于复杂问题（如围棋）的标注，人类的标注有时并不一定是最佳选择。很多时候，人类高手容易出现盲点。而强化学习算法，因为不依赖太多先验知识，反而能够跳出窠臼。所以，AlphaGo Zero的有些落子，出现了一些“神之一手”，人类顶级选手都想不到的招数。

除了为强化学习注了一剂强心针之外，Alpha Zero还号称，通过这种从零开始的强化学习，它可以学习到已有的和新的围棋定式，也就是说学习到了新的知识。而定式是通过出现频率来判断的。这点也非常有意义，因为这再次表明了显式的知识可以通过隐式的（学习）过程来得到，而且这种过程能得到以前从未有过的知识。虽然这很振奋人心，但目前还需要持辩证的观点。例如，基于出现频率来判断知识是不是靠谱（如有些频率出现高的未必就能称为知识）？以及这些新得到的定式是否真的很有用？这两点在文章中并没有详细分析。

总而言之，AlphaGo Zero攻克了智力游戏中的皇冠——围棋；提出了一个新的“基于蒙特卡洛树搜索的强化学习”方法来估算搜索中的评价函数；验证了强化学习的有效性；进一步表明用隐式的方法能够获取显式的知识，当之无愧是人工智能史上一个里程碑。

最后，在祝贺AlphaGo Zero团队成功的同时，尝试分析一下其成功的原因。首先，不积跬步，无以至千里，AlphaGo Zero的主要成功在于长期的积累。其主要作者们长期致力于围棋程序，并在蒙特卡洛树搜索和深度学习下围棋两方面都有建树，把这两者结合起来是一个水到渠成的事情。其次，该团队敢想敢做，敢于去挑战围棋这个皇冠，这点非常值得学习和敬佩。因为这类工作往往风险很大，至少从发文章的角度来讲，远不如修修补补的改进工作来的容易。再者，该团队工程能力相当强大。对于这样的工作，写在文章里的只是背地里汗水的沧海一粟。在实现上，一定趟过了相当多的坑。当然，Google Deepmind的鼎力支持也是不可或缺的因素。

[1] Mastering the game of Go without human knowledge. D. Silver, J. Schrittwieser, K. Simonyan, I. Antonoglou, A. Huang, A. Guez, T. Hubert, L. Baker, M. Lai, A. Bolton, Y. Chen, T. Lillicrap, F. Hui, L. Sifre, G. van den Driessche, T. Graepel, and D. Hassabis. Nature 550 (7676): 354--359. 2017.

[2] Mastering the game of Go with deep neural networks and tree search. D. Silver, A. Huang, C. J. Maddison, A. Guez, L. Sifre, G. van den Driessche, J. Schrittwieser, I. Antonoglou, V. Panneershelvam, M. Lanctot, S. Dieleman, D. Grewe, J. Nham, N.Kalchbrenner, I. Sutskever, Ti. P. Lillicrap, M. Leach, K. Kavukcuoglu, T. Graepel, D. Hassabis. Nature 529(7587): 484-489. 2016.

[3] https://en.wikipedia.org/wiki/Chinook_(draughts_player).

[4] https://en.wikipedia.org/wiki/Deep_Blue_(chess_computer)

[5] Monte-Carlo tree search and rapid action value estimation in computer Go. S. Gelly, D. Silver. Artificial Intelligence. 175(11): 1856-1875. 2011.

[6] http://www.image-net.org/

[7] https://catalog.ldc.upenn.edu/ldc2012t13