哼，又拿这些词儿唬我，我就去查了一下什么叫做“随机行走”。

经典随机行走——期望值（距离）²=步数

说起随机行走，可能你并不陌生，中学的时候，你一定学过一种物理现象——布朗运动。1827年英国植物学家R.布朗在花粉颗粒的水溶液中观察到花粉不停顿的无规则运动。花粉在水中，因为受到的不同方向的力并不平衡，导致了它们的无规则运动，这是一种分子热运动的宏观表现。后来很多科学家研究过这种现象，1905年的时候，“爱神”爱因斯坦就深入分析过布朗运动的理论[1]，随机行走的物理图像开始被人们广为接受。

为了简单地理解经典随机行走，我们可以想象一个一维的格子。

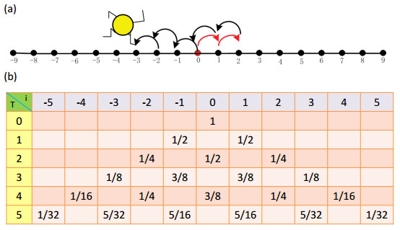
（图片来源：大可数学人生工作室《量子行走漫谈》）

假设一个粒子本来待在坐标0点处，每过一个单位时间，它就会走一步——但是它走得很随机，一半概率向左走，一半概率向右走。当它到了下个点（-1或者1）之后，接下来的走法还是如此——一半概率向左走，一半概率向右走。将前五步的可能性画出来，就是上面的图（b)。当然，数学家早就算好了接下来所有的可能性，而且，在这个模型里，粒子离开原点距离的期望值等于步数^1/2。现在，小墨明白为什么这些大牛说要专注了，一个人拼命往一个方向走，离开原点的距离就等于步数，要是走得太随机，就只能走步数^1/2了。本来小墨被打击地体无完肤，但是，研究院的大牛们纷纷安慰小墨：“不要着急，其实，有一种行走虽然随机，但是也可以走出精彩。这就是——量子行走”。

千变万化的量子行走

如果咱们把上面的一维行走放到量子世界里，情况就变得更奇异了。因为量子世界里的粒子遵循量子叠加、量子干涉等规律，它们的行为会变得很复杂。比如，在量子随机行走中，粒子可以同时既往左边走又往右边走，形成鬼魅的“分身”（两边的概率幅可以相同，也可以不同），而且，粒子的“分身”之间彼此还可以相互干涉。如果这个一维的格子上有不止一个粒子，彼此之间叠加和干涉，随着时间的演化，会形成更加复杂的行为。此外，粒子种类不同，相互作用方式也不同，那么在晶格上的量子行为会大相径庭。这些都吸引了科学家的研究兴趣。有人认为，在量子处理器上进行量子行走的演示，是实现量子计算的一条重要途径。

可是，在量子系统中演示量子行走不是容易实现的。时间上，要做到能保持长的相干时间，空间上也要保证不同格点上的粒子“分身”有很好的耦合。整个系统还要能被我们有效、精确的控制，并且可以扩展。近年来，离子阱系统、光学系统都在量子行走演示上做出过一定尝试。

12比特超导系统的表现

既然说到量子计算，那我们曾经提到的超导系统当然要上阵磨枪啦。中国科大上海研究院的科学家们手中的超导比特这次就演示了一把。

科学家们建造了一个12比特的超导处理器，他们将12个超导量子线路排成一维的晶格。这些量子比特可以看做一种人工原子，像天然原子一样激发出准粒子，准粒子的行为可以看成光子。这些超导量子比特具有较长的寿命（退相干时间），而且还可以被精确地操作，以及读出。看，这就像一个小小的处理器了不是吗？ 

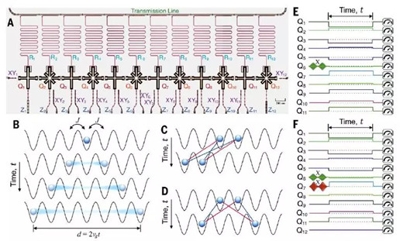
（12比特超导量子处理器芯片及实验原理图、实验流程图。图片来源：Science文章正文。）

在这个实验中，光子的量子行走是在一维阵列上进行，光子是玻色子，玻色子在一维的相互作用可以根据Bose-Hubbard模型进行描述[2,3,4]。科学家想看看，光子在这个阵列上的行走是不是真的符合Bose-Hubbard模型。

首先，科学家观察单个光子的量子行走。一维阵列编号从Q1~Q11（11比特）,这个光子初始位置被安排在中间的Q6，随着时间演化，科学家观察了不同时刻、不同格点位置上的光子密度分布，和Bose-Hubbard模型很好的吻合。后来，光子初始位置被安排在两边的Q1和Q11，情况也与理论相符。有趣的是，光子在一维阵列上开始变得活泼起来，它舞动着着手中的绸布，利用干涉和反射作用，变化出主波、次级波和回波，在一维方向上，光子密度呈现出有趣的波动舞蹈。

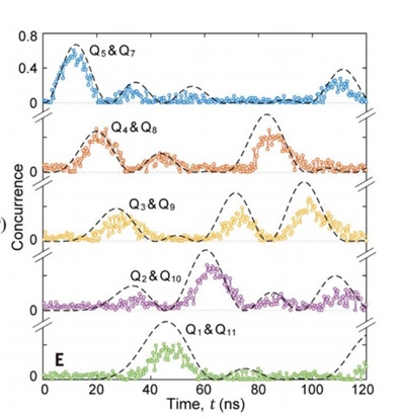
（一对两比特间的量子纠缠随时间演化展现的纠缠传递行为，得益于超导量子芯片的长退相干时间和高保真度操控及读取，纠缠传播中的主波、次级波及回波现象均被观察到。图片来源：Science文章正文。）

后来，科学家又在阵列上加了一个光子。他们想看看两个光子又能如何变化多端。这次的一维晶格有12位，编号为Q1~Q12。两个全同的光子先是被分别放在了最中间的Q6点和Q7点，科学家同样观察了不同时刻、不同格点位置上的光子密度分布。由于光子之间的强关联作用，神奇的事情出现了。与自由光子行为明显不同，两个光子的空间密度呈现反相关性，好像一种类似费米子的行为，这是由于两个光子之间的强相关性，产生的一种反聚束效应。当然，这些表现都与理论预言一一相符。

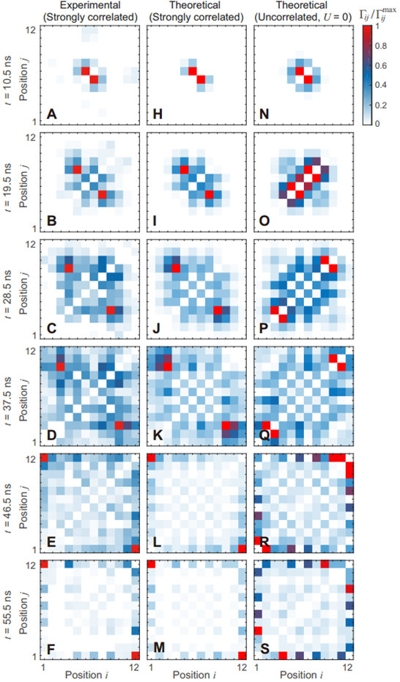
（强关联及非关联光子体系的双光子激发量子行走过程中二阶关联函数随时间的演化过程。左、中两栏分别为实验及理论得到的强关联光子体系的演化，而右栏展示的是非关联光子体系的理论演化。通过对比，可以清晰地观察到强关联光子体系二阶关联传播方向与光子运动方向相反的奇异现象。图片来源：Science文章补充材料）

  2019年5月2日，这篇题为“Strongly correlated quantum walks with a 12-qubit superconductingprocessor”的研究论文在Science在线发表，由中国科学技术大学潘建伟、朱晓波和彭承志等人组成的超导量子实验团队，以及中国科学院物理研究所范桁等人的理论小组合作完成。在12比特的超导处理器上，他们分别研究了单个和两个强关联光子的连续时间量子行走，观察到了基本量子效应，包括叠加态量子信息的光锥传播，特别是量子比特对之间的纠缠传播现象，以及时间演化相关的奇异行为、强关联光子的费米子化和反聚束现象。

  总而言之，该研究通过实验研究了具有短程相互作用的一维超导量子比特阵列中的一个和两个强相互作用光子的量子行走。接下来，研究结果可以扩展到几十个量子比特，为进一步研究多体动力学现象和通用量子计算奠定了基础。

我们可以畅想一下这样的量子计算机可以用来做什么。生活中，可不止小墨和布朗的花粉酷爱随机行走，其实，许多生物过程、化学反应都离不开量子行走的模拟计算。甚至，经济学中很多理论基础就来源于随机行走，比如，基于随机行走思想的Black-Scholes期权定价理论还获得了1997年诺贝尔经济学奖呢。

  经典行走其实早就被用在设计随机算法中。2001 年， Ambainis, Kempe 和 Childs 等人提出可以利用量子随机行走开发量子计算算法[5，6]，这样，对很多经典方法中比较困难和低效的问题都可以提供量子加速性。

  小墨暗搓搓的想，等这样的量子计算机开发出来，谁还能说随机行走太随机、走不远呢？

（龚明亦对此文的完成有贡献）

原文链接：https://science.sciencemag.org/content/early/2019/05/01/science.aaw1611

参考文献：

[1] A. Einstein, The motion of elements suspended instatic liquids as claimed in the molecular kinetic theory of heat. Annalen derPhysik 17(8): 549-560 (1905).

[2]P.Roushan, C. Neill, J. Tangpanitanon, V. M. Bastidas, A. Megrant, R. Barends, Y.Chen, Z. Chen, B. Chiaro, A. Dunsworth, A. Fowler, B. Foxen, M. Giustina, E.Jeffrey, J. Kelly, E. Lucero, J. Mutus, M. Neeley, C. Quintana, D. Sank, A.Vainsencher, J. Wenner, T. White, H. Neven, D. G. Angelakis, J. Martinis,Spectroscopic signatures of localization with interacting photons insuperconducting qubits. Science 358, 1175–1179 (2017).

[3]M. A.Cazalilla, R. Citro, T. Giamarchi, E. Orignac, M. Rigol, One dimensionalbosons: From condensed matter systems to ultracold gases. Rev. Mod. Phys. 83,1405–1466 (2011).

[4]J.Koch, T. M. Yu, J. Gambetta, A. A. Houck, D. I. Schuster, J. Majer, A. Blais,M. H. Devoret, S. M. Girvin, R. J. Schoelkopf, Charge-insensitive qubit designderived from the Cooper pair box. Phys. Rev. A 76, 042319 (2007).

[5]A.Ambainis, E. Bach, A. Nayak, A. Vishwanath, J. Watrous,One-dimensional quantum walks. in Proceedings of the thirty-third annual ACMsymposium on Theory of computing. pp. 37-49 (ACM New York, New York, 2001).

[6]D.Aharonov, A. Ambainis, J. Kempe, U. Vazirani, Quantum walks on graphs. in Proceedingsof the thirty-third annual ACM symposium on Theory of computing. pp. 50-59 (ACMNew York, New York, 2001).