内容来源 | 中国科普博览

作者 | 袁岚峰

2017年9月29日，世界首条量子保密通信干线“京沪干线”正式开通。这是中国继2016年8月16日发射世界第一颗量子科学实验卫星“墨子号”后，在量子保密通信领域的又一项重大进展。对于京沪干线的介绍，可以参见我的文章《解读量子通信京沪干线，包你懂》（https://mp.weixin.qq.com/s/30ucPReX9Z7gI1SmIcINog）。

我的前辈朋友、加州大学洛杉矶分校（UCLA）物理系研究员徐令予，在退休后很关心中国科技各个领域的发展，近年来在观察者网和科学网等媒体写了许多文章，介绍和评论的领域十分广泛，遍及量子信息、航天、天文望远镜、人工光合作用、太阳能发电、无人驾驶等等（http://www.guancha.cn/XuLingyu）。包括我在内的读者们从中学到了很多东西，也对美国的社会动态增加了很多了解。对于各个具体科学问题，即使意见不是完全一致（例如对于500米口径射电望远镜FAST），我们也可以看出徐老师对故乡和同胞的眷恋，对此都抱有深深的敬意。虽然我和徐老师尚未谋面，不过在网络上已经做过不少交流，可以称为忘年交了，对此我深感荣幸。

因此，当我看到徐老师2017年10月31日发表在观察者网的文章《炒作量子通信工程，连潘建伟都担心》（http://www.guancha.cn/XuLingyu/2017_10_31_432886_s.shtml）时，认为这是一篇值得仔细研究的文章。此文在开头祝贺了京沪干线开通后，侧重点就急转直下，主要篇幅放在给量子保密通信泼冷水降温上。

为什么说这是急转直下呢？因为徐老师以前的许多文章，是对量子保密通信的科普和支持，例如《为什么发展量子密钥技术已刻不容缓》（http://www.guancha.cn/XuLingyu/2016_08_19_371818.shtml）、《为什么说外国无法破解中国量子密钥技术》（http://www.guancha.cn/Science/2016_08_16_371382.shtml）、《反对高铁的逻辑，要用到量子通信上了？》（http://www.guancha.cn/XuLingyu/2016_08_26_372499.shtml）。

从这些文章中摘几段：

“量子计算机的研发进展是各强国的最高机密，媒体上的报道真真假假千万信不得，很有可能用以破译的专用量子计算机已经接近完工，这决不是危言耸听，密码世界从来是波诡云谲、莫测高深。即使按专家们保守的预测，量子计算机的实际应用也许还要等十到十五年，但寻找新的密码系统，特别是开发密钥分配的新技术已经刻不容缓，因为新技术从开发到系统的建立和实用也需要时日，所以我们已经到了最危险的时刻！”（《为什么发展量子密钥技术已刻不容缓》）

“有必要再次强调：与其它密码技术不同，量子密钥分配技术从原理上保证密钥配送是绝对安全的，量子通信是稳定可靠的，加速发展量子通信是十分必要的，因为现有密码系统已经到了最危险的时刻。工程实施中一定会有许多的问题，但原理与实施是完全不同的两个概念，毕竟实施中的技术问题可以逐步解决，不可破译的原理才是该项技术具有发展前途的根本保证，它使我们对量子密钥分配技术的将来充满了信心。”（《反对高铁的逻辑，要用到量子通信上了？》）

以上这些说法，我都十分赞同。而在《炒作量子通信工程，连潘建伟都担心》一文中，徐老师的结论却似乎翻了个个：

“开发量子保密技术为的是应对未来可能发生的危机，但这种危机离我们仍十分地遥远，即使危机真的降临，改进升级后的经典密码系统应该足以应付危局。量子密码技术并非是对抗危机的唯一选择，它很有可能仅是一枚永远也使用不上的备胎。”

有意思，大反转啊！当然，徐老师在此文中一再声明：“对量子保密通信技术作前瞻性科学研究应该大力支持，我的这个态度始终也不会改变。”不过对工程的态度，看起来徐老师是反转了。

类似的观点我早就看到过，但那些并不值得认真对待，因为只有个结论，没有论证过程。而徐老师就不一样了，无论他写什么话题，持什么观点，总是会举出不少“干货”，无论正方反方都可以从中得到新的信息。在这篇文章中，最大的干货是一篇标题为《后量子RSA》（“post-quantum RSA”）的论文（https://eprint.iacr.org/2017/351.pdf），徐老师向大家介绍了这篇论文，把它作为经典密码术已经够用的重要证据。

徐老师把这篇20页的论文发给了我，最近我仔细研读了一番。我的专业是理论与计算化学，量子力学是这门学科的基础之一，所以我对量子力学还算是比较熟悉，但是对信息科学的了解就很有限了。至于密码学这门需要大量数学技巧的学科，我更是门外汉。不过，经过研读，加上一些专家朋友的帮助，我想我还是理解了《后量子RSA》的基本框架。

这篇文章确实很有趣，提出了一种比现在通行的RSA密码体系更加能够抵抗量子计算机的改进版RSA。但在理论层面，这个进步只是把“完全不安全”（敌方破解几乎跟合法用户解密一样快）提升到了“稍微有点安全可言”（破解的速度低于加密解密的速度），远远没有达到正统的安全标准（破解的计算量指数增长）。更重要的是，这个进步跟“量子密码术为什么有价值”的大图景完全无关。这样的进步再来一万个，也不会使经典密码术变得无懈可击，不会使量子密码术变成多此一举。其实作者们也完全没有这个意思，原文对这个成果的自我评估是很准确的，徐老师似乎对这篇论文有些误读。其中一个误读是，把“2的100次方的量子比特操作”看成了“2的100次方的量子比特”，由此引申出来的评论自然也都失准了。

徐老师文章中的论据，除了《后量子RSA》之外，还有其他的。不过在我看来，有一些比较明确的错误（“硬伤”），还有一些比较“软”的可商榷之处。其中最硬的错误，是认为有些公钥密码体系已经在原理上被证明不可能被量子计算机破解了。实际上，人们还没有证明任何一个公钥密码体系不可能被经典计算机破解，又怎么可能得到更强的结果，证明它不可能被量子计算机破解呢？

一个公钥密码体制可以抵抗某种算法的攻击（包括量子算法），不等于能从原理上证明其安全性，因为后者是要证明它可以抵抗任何已知和未知算法的攻击。而至今唯一能从原理上严格证明安全性的密码体制，就是量子密码术。这是量子密码术与所有的公钥密码体制之间的根本差別。

在一篇文章里见到这么多可商榷之处，对于低水平的作者来说很常见，对于徐老师来说很罕见。我感觉这篇文章徐老师写得比较急促，大概是心里对另外一些事感到焦虑，一些科学之外的事。我跟徐老师沟通，徐老师告诉我，被最近某公司人身威胁科学家的事件刺痛了，最担忧的是骗子伤了众人的心，最后政府光火把脏水连同孩子一起泼出去，所以希望理性降温。这就可以理解了。对于如何保持量子通信领域的健康发展，我也将在本文中谈谈我的观点，以及我了解的一线工作者的看法。公众、投资者和潜在的用户明白了这些基本图景，也将有利于抵制资本与媒体的炒作，促进量子通信行业健康发展。

以上是一个总体的介绍。下面我来具体说明各个要点，以及借这个机会，解释一个基本问题：量子密码术的价值究竟在哪里？

什么是量子密码术？

描述微观世界基本物理规律的理论，叫做量子力学，它跟相对论是目前已知的两大基础物理理论。量子力学出现后，我们就把描述宏观世界的牛顿力学称为经典力学，它可以理解为量子力学在宏观情况下的近似。

1980年代以来，量子力学跟信息科学交叉，产生了一门新的学科“量子信息”。这门学科的目的，就是利用量子力学的特性，实现传统信息科学中实现不了的功能，例如永远不会被破解的保密方法（就是后面要解释的量子密码术）、科幻电影中的“传送术”（它的专业名称叫做“量子隐形传态”）。

《星际迷航》中的传送术

经典的信息科学包括通信和计算两大主题，量子信息的研究内容同样也可以分成两大块：量子通信和量子计算。这两大子领域里又各自有若干具体应用，刚才说的量子密码术和量子隐形传态都属于量子通信，而量子计算中的重要应用包括量子因数分解和量子搜索等等。下面这个图，可以表示量子信息这门学科的脉络。

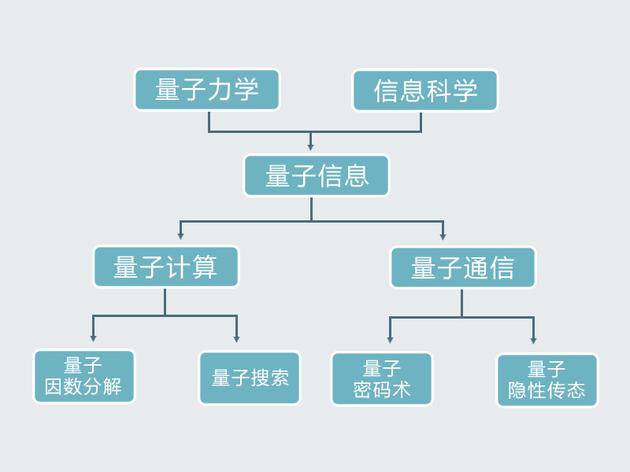
量子信息学科内容

我写过不少量子信息的科普文章，目前最全面的一篇是应新浪科技之邀写的《你完全可以理解量子信息》（http://tech.sina.com.cn/d/2017-08-31/doc-ifykpysa2199081.shtml）。读者如果想知道量子力学有哪些可以用于信息科学的特点，量子信息的这些应用做的是什么事，以及为什么能做到，请去参阅这篇长文。

许多媒体在报道“量子通信”如何如何的时候，指的实际是量子密码术，即量子通信的一部分而非全部。量子密码术又被称为“量子保密通信”或者“量子密钥分发”，无论从哪个名字，你都可以一眼看出，它是一种保密的方法，不是有些媒体胡思乱想的超时空传输之类。

量子密码术实际做的是什么事情呢？简短的回答是：不通过信使，让通信双方直接分享密钥。打个比方，就是《红灯记》中的李玉和下岗了，地下党和游击队不通过他就直接获得了同一套密电码。

《红灯记》

怎么做到的？有若干种技术方案，都称为某某协议，包括BB84协议、E91协议、B92协议、诱骗态协议等等。由于篇幅所限，本文对这些方案不能详细解释。有兴趣的读者，请参阅《你完全可以理解量子信息》中的相关内容
（http://mp.weixin.qq.com/s/kKLd5_YbjI765qBvuSFB4A）。

这里有一点值得强调。许多科普作品说量子密码术离不开“量子纠缠”（你八成听说过这个词），但这个说法是错误的！一线工作者都知道它错，而媒体仍然整天这么说，——可能他们觉得量子纠缠这个词比较高大上，读者听了以后晕头的程度直接上升三级。实际情况是，量子密码术有若干种实现方案，有些用到量子纠缠，有些不用量子纠缠。量子纠缠是个可选项，而不是必要条件。

不仅如此，量子纠缠其实还是个很少被选中的可选项。量子纠缠是一种多粒子体系的现象，而对于实验来说，操纵一个粒子肯定比操纵多个粒子容易。量子密码术可以通过发射和接收单个光子实现，所以，绝大多数量子密码术的实验都是用单光子方案做的，这样达到的效果更好。有些文章通过批评量子纠缠来批评量子密码术，这其实就是被那些说量子密码术必须用到量子纠缠的媒体给忽悠了，属于无的放矢。 

量子密码术为什么有价值？

不通过信使，让通信双方直接分享密钥，这显然是个非常奇妙的能力，是以前想象不到的。不过，这个能力有什么样的意义？这就需要从密码学的基本框架讲起了。

把明文变换成密文，需要两个元素：变换的规则和变换的参数。前者是编码的算法，后者是密钥。密码学的一个基本原则是，在设计算法时，你必须假设敌人已经知道了算法和密文，唯一不知道的就是密钥。

用一个比喻来说，密码学的攻防就好比魔王追公主（魔王：“你喊吧，喊破喉咙也不会有人来救你的！”破喉咙：“公主，我来救你！”）。魔王知道公主运动的规则，但不知道公主运动的参数。魔王的目标是在这种前提下追上公主，公主的目标是在这种前提下摆脱魔王。

我们经常说，没有完美的东西。但在理论的层面上，这话其实不对。有一种很简单的密码体系，就具有“完美的安全性”（perfect security）。这里的“完美安全”是个信息论的术语，意思是攻击方无论有多强的计算能力，都不可能从密文中得出任何信息。

这话听着似乎很玄，实际的意思却很简单。假如你要传一比特的信息（即0和1这两个数中的一个），密钥也有两个选择：0和1。算法非常简单：如果密钥为0，那么密文就等于明文，即把0变成0，把1变成1；如果密钥为1，那么密文就是0和1中不同于明文的那个数，即把0变成1，把1变成0。学过二进制的同学们知道，这个算法就是“模为2的加法”。现在如果你告诉敌人密文是0，那么他能得到什么呢？什么都得不到！他唯一可说的，是明文有一半的可能是0，一半的可能是1。但这是句废话，因为如果密文是1，这句话同样也成立。他不看密文就知道这一点，看了以后也不能增加任何新知识，所以这个密码体系就是不可破译的，具有完美的安全性。

当然，这是个最简单的例子，只适用于明文长度为1比特、只传输一次的情况。把这个办法推广到更长的明文长度、更多次的传输，需要满足三个条件。哪三个条件呢？一，密钥的长度跟明文一样；二，密钥是一串随机的字符串；三，每传送一次密文后都更换密钥，即“一次一密”。满足这三个条件的密钥叫做“一次性便笺”（one-time pad）。信息论的创始人香农（Claude E. Shannon）从数学上证明了：密钥如果满足这三个条件，通信就是完美安全的。这个定理可以称为“系统的安全保密性定理”。

香农

一次性便笺保密的实质，是让密文跟明文完全没有关联，任何的密文都以相等的概率对应相同长度的任何的明文。好比你问一群村民：“李向阳在哪里？”所有人都回答：“我就是李向阳！”在魔王追公主的故事中，就好比公主下一步可以跳到任何地方，“瞻之在前，忽焉在后”，完全无法预测。这让魔王怎么玩？魔王：“算你狠！破喉咙，你把公主带走吧！”破喉咙：“公主已经上天了，我也找不着她……”

这么说起来，保密的问题已经解决了？

其实没有！

真正的难题在于，怎么让双方共享密钥？在量子密码术出现之前，密钥需要第三方的信使来传递。而信使可能被抓（如《红灯记》中的李玉和），也可能叛变（如《红岩》中的甫志高），这麻烦就大了。现在甚至都有技术可以远程读出未通电的硬盘里的数据，传送密钥这活越来越不好干了！

甫志高

因此，在很长时间内，一次性便笺保密法的意义主要是在理论上，用来证明完全保密的系统是存在的，而实践意义很小。道理很明显：一次性便笺密钥跟你要传输的明文一样长，如果你能安全地传输这么多的密钥，那用这个信道直接传输明文不就得了？不就是因为没有这么安全的信道，才需要发展保密方法吗？这就好像周星驰的电影《国产凌凌漆》里那个“有光照才会发光的手电筒”，成了一个一本正经的笑话。

魔王长出一口气：来来来，公主，我们重回赛场！

密码学家们也不会轻易地狗带，他们开辟了另外一个战场，叫做“公钥密码体制”。公钥的意思，就是这个密钥是向全世界公开的，所有人都可以看到。还有一个私钥，只在接收方（以下称为B）手里有，发送方（以下称为A）手里没有。用公钥可以加密，但不能解密，用私钥才能解密。因此，A把明文用公钥加密后，公开传给B，别人截获了没有私钥无法窃密，而B拿到了就可以解密。公钥密码体制也常常被称作“非对称密码体制”，因为双方手里的密钥不一样多。而双方共享同一套密钥的方法就叫做“对称密码体制”，一次性便笺就是其中的一种。

公钥密码体制的关键在于：通过某些数学操作可以方便地从公钥得到私钥，但从公钥却很难得到私钥。也就是说，有些数学问题沿着一个方向操作很容易，沿着相反的方向操作却非常困难，“易守难攻”。

因数分解就是一个典型例子。把两个质数相乘得到一个合数，是很容易的，而把一个合数分解成质因数的乘积，例如291,311 = 523 × 557（到下一节你就会明白为什么举这个例子），就难得多了。

让我们想想，如何分解一个数字N。最容易想到的算法，是从2开始往上，一个一个地试验能否整除N，一直到N的平方根为止。如果N用二进制表示是个n位数，即N约等于2的n次方，那么尝试的次数大致就是2的n/2次方。指数上出现n，这就麻烦了，这叫做“指数增长”。学过微积分的同学们明白，指数增长是一种极快的增长，比n的任何多项式都快。比如说，2的n次方比n的10000次方增长得还要快。没有学过微积分的同学也不要头晕，看看下面的图就可以明白这个意思。

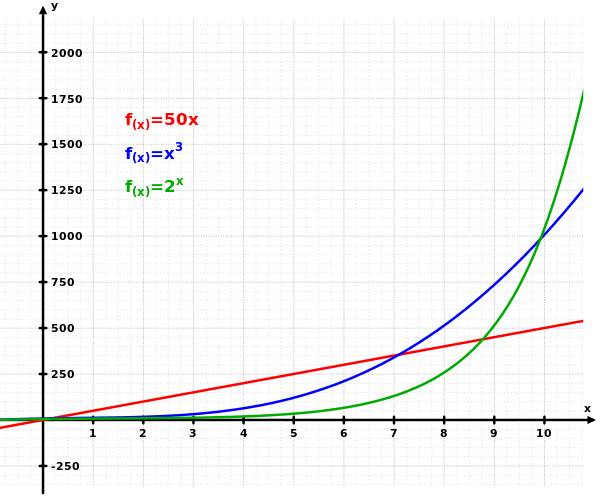
指数增长的威力。指数函数虽然在最初落后，但很快势不可挡地超越了线性函数和三次方函数，而且越到后面把它们甩得越远

在多项式之间比较，当然是次数越高增长得越快，例如n的三次方比二次方快，二次方比一次方快。但在计算机科学中，多项式内部的这个差别并不太重要，它们只是定量的差别（医生，我觉得我还可以抢救一下），而指数增长与多项式增长的差别是定性的差别（同志，放弃治疗吧……）。因此，计算机科学中把计算量多项式增长的问题称为“可解的”（tractable），把计算量指数增长的问题称为“不可解的”（intractable）。不可解的意思并不是计算机不能算，而是计算量增长得太快，通过扩大问题的规模，很快就能达到“用全世界的计算机算几十亿年都无法得出结果”的程度。

当然，你可以寻找效率更高的算法。对于因数分解，人们发展了很多种比“一个个试”聪明得多的算法。但到目前为止，这些算法的计算量仍然都是指数增长的。

1978年，基于因数分解的困难性，三位密码学家李维斯特（Ron Rivest）、萨莫尔（Adi Shamir）和阿德曼（Leonard Adleman）发明了“RSA密码体系”（这个名字是他们的首字母缩写），这是现在世界上最常用的公钥密码体系之一。

RSA密码体系的三位发明者

除了RSA之外，还有许多其他的公钥密码体系。无论哪种，基本思想都是一样的，安全性来自某个数学问题的困难性。回到魔王与公主的比喻，现在公主不是满世界乱跳了，而是按照某种确定的规则前进。魔王以前是完全无从追起，而现在有可能追上公主了，只要解出某个数学问题就行。但是这个数学问题的计算量是指数增长的，通过扩大问题的规模，很容易就使解题所需的时间变得不可思议的长（指的是计算题，不是五点共圆这种证明题）。魔王：为什么一定要解数学题，我们来比写诗吼不吼啊！

公钥密码体系是个伟大的发明，但它达到完美的安全性了吗？显然没有，因为完美安全性的意思是无论敌方有多强的计算能力都不能破解。魔王：跟你说解数学题不好了嘛，我先来念两句诗……

在这个前提下，如果我们退一步，把计算量指数增长作为仅次于完美安全的第二级别安全性，那也可以接受。但在这个台阶上，问题又来了：你怎么能保证对这个数学问题，不会发现多项式计算量的算法呢？

实际上，计算机科学中的一大难题就是：我们可以证明，计算量指数增长的问题有很多，然而，我们几乎无法确定任何一个具体的问题属于这一类！

包括因数分解在内，目前公钥密码体制用到的所有数学问题都是这样，无法排除哪天有人提出破解算法的可能。因此，密码学处于一种无止境的军备竞赛对抗之中，一方提出更强的攻击算法，另一方提出更强的保密算法，无限地循环下去。

算法的进步和硬件的进步，迫使许多公钥密码体系一再升级。例如RSA推荐使用的质数长度，就在不断增加。即使你升级了，也只能保护新的数据，许多历史数据还是可以被破解的，这又是一重头疼。

以上这些，都是基于对公开算法的讨论。但是，只有学术界才会把破解的消息公开。在实际的军事、政治、经济对抗中，对手如果破解了你的密码，会让你知道吗？偷袭珍珠港的策划者山本五十六是因为行程泄露，飞机被美国击落而死的，难道美国会告诉日本“我已经破解了你的密码”吗？

在拍摄此照片几小时后，山本五十六就被击毙

早就有一位长者说过：你们啊，naive！闷声发大财才是坠吼的！

用《三体》的语言说，你无法判断对方是否破解了你的密码，这就构成了“猜疑链”。用美国前国防部长拉姆斯菲尔德的语言说，最可怕的就是“未知的未知”。

拉姆斯菲尔德和“未知的未知”

在量子密码术出现之前，永远的猜疑、无尽的升级和不时的泄密是我们不得不忍受的代价。毕竟，一次性便笺是个中看不中用的银样镴枪头，真正能用的最好的保密方法就是公钥密码体制了。

“那是一个涉密的科研项目，我们团队发明了一种三重MARS加密算法，我们认为比上级配发的传统加密方法更安全。

由于密码算法的使用必须得到国家和军队某委员会的批准，因此我们向他们提出了鉴定申请，结果却被驳回。

我对此不服，给他们说：你们凭什么认为我这个算法不够安全，有本事你们破解试试？

他们的回答是：我们没本事破解，但不代表敌人没本事破解，你给我证明下敌人无法破解。

然后我就懵逼了，最后只能继续使用上级配发的加密算法，这样即使出了问题也没我的责任。

加密算法就是这样，你很难证明它安全，也很难证明它不安全。

加密算法的强度依赖的是数学难题的难度，即使是大家公认的极难解决的数学难题，也备不住躲在阴暗角落的某个天才数学家已经破解，而数学问题的破解就如同窗户纸一样，一捅破就全完了。

很可能敌方已经据此设计了完美的破解方法，这种可能虽然可能性极小，但终归无法杜绝！因此，在传递绝密信息时，谁都不敢拍胸脯保证，只能去赌概率，这是令人非常非常痛苦的！”

现在，我们的主角出场了。量子密码术，改变了密码攻防的基本格局。

我就是美貌与智慧并重，英雄与侠义的化身：唐伯虎

不通过信使，让通信双方直接分享密钥，这意味着什么呢？意味着原本只具有理论意义的一次性便笺保密法起死回生了，变成一个可以实用的方法了！这种保密方法，封死了通过数学破解密码的可能性！

因此，“奥卡姆剃刀”在讲完上面那个故事之后，结论是（https://www.wukong.com/question/6471509815406362893/）：

“而量子通信解决了这个问题，它从理论和实践上都证明了不可破解，令人把悬着的心放回肚里，这是上千年密码术的重大突破，功莫大焉！”

回到魔王与公主的比喻，现在公主又变成了满世界乱跳，而且这次可以放心大胆地这么做了！魔王彻底失去了追上公主的希望，无论他的计算能力再强都无济于事。因为，这压根就不是计算的事儿。

魔王：算你狠，我举白旗还不行吗？我看看还有没有其他的办法……

量子密码术的出现，并不意味着信息安全的问题已经完全解决了。最明显的，策反情报人员这一招就仍然存在。我的朋友、美国新墨西哥大学数学与统计系助理教授黄宏年博士认为，现在网络安全体系最大的弱点并不在于密码，在这方面增强不能解决主要问题。现在的操作系统过于复杂，许多地方用溢出攻击等粗浅的手段就可以攻破。

我的理解是，信息安全问题是个很长的链条，量子密码术只是保证了其中一个环节的安全，即密钥分享和密文传送这一环，敌方仍然可以去攻击其他的环节。但是，能保证一个环节的安全已经是相当重大的进步了，至少你泄密时可以排除这方面的问题，集中排查其他方面。正如中国工程院院士邬江兴所说：中国的网络安全几乎是“裸奔”，量子密码术给它穿上了一条内裤。

如果你问我，量子密码术有什么缺点？最明显的，就是慢。由于密钥是通过单光子的发射和接收产生的，条件十分苛刻，所以生成密钥的速度目前都是在每秒多少k的量级。在一次性便笺加密中，明文跟密钥一样长，所以传输信息的速度就等于生成密钥的速度。每秒不到一兆的速度就像回到了拨号上网用“猫”的时代，只能传送少量最重要的文本。如果用AES、DES之类不等长加密的对称密码算法（用一段密钥加密一个长得多的文件），速度倒是上去了，但又有可能被数学破解了。此外，量子密码术的成本应该也不低，虽然我没有具体数据。

除了慢和贵之外，作为一个新技术，量子密码术的问题想必还有许多。不过我既不是工程专家，也没有打算自学成一个工程专家（估计学也学不成），我的兴趣主要在理论方面，因此对我来说，最重要的是：量子密码术的安全性是能在原理层面证明的，而目前其他的密码体系都不能。这就是量子密码术无可替代的价值。

由此还可以引出一点值得强调的：量子密码术从来没有说要完全代替传统的密码术。作为一个新生事物，量子密码术不是一上来就宣布“这个鱼塘我承包了”（正经的科技工作者不会这样说话的），而是“我有这样一个能力，可能对保密有用，欢迎大家一块来讨论，看看什么地方能用上”。你可以列举一千个不适合用量子密码术的地方，这都没问题，但只要有一个地方适合用量子密码术，就算是进步了。用了量子密码术，也不意味着排斥经典密码术，双方完全可以结合使用，取长补短。

用不用量子密码术的选择权，当然在于用户。如果你对保密的要求高于一切，那么量子密码术是你的好选择。如果你没有高价值的秘密需要保护，那有什么理由像某些企业宣传的那样，花很高的成本去追逐“量子小镇”之类的噱头呢？

量子计算机对这幅图景有什么影响？

基本的回答是：非本质的影响。你看，我前面说了那么多，压根就没提到“量子计算机”这个词嘛！

传统计算机的基本单元是比特（bit），指的是一个体系有且仅有两个可能的状态，往往用0和1来表示。而量子计算机的基本单元是量子比特（quantum bit，缩写为qubit或qbit），指的是一个体系可以处于两个状态|0>和|1>以及它们的任何叠加态a|0> + b|1>。这里的|>叫做狄拉克符号，在其中填入数字或文字，就可以表示量子状态。

做一个比喻：经典比特是“开关”，只有开和关两个状态，而量子比特是“旋钮”，有无穷多个状态。因此，量子计算机可以做到所有的经典计算机可以做的事，还有可能做到一些经典计算机做不了的事。

这里需要强调一点，常有文章把量子计算机描写成无所不能，都快成神了，这是重大的误解。量子计算机仍然是需要算法的，而只对于某些特定的问题，人们才设计出了超越经典计算机的算法。因此，量子计算机不是因为普遍性的算得快，所以干什么都比经典计算机强，而是针对某些特定的问题算得快，只在这些问题上比经典计算机强。

到目前为止，人类找到的这样的问题并不是很多。但在这为数不多的能够让量子计算机大展拳脚的问题中，其中一个恰恰就是——因数分解。

前面说对因数分解，迄今还没有能在多项式时间内分解的算法，但那指的是经典计算机。1994年，肖尔（Peter Shor）发明了一种量子算法，把因数分解的计算量减少到了多项式级别。这是一个革命性的进步！分解300位和5000位的数字，量子算法会把所需时间从15万年减到不足1秒钟，从50亿年减到2分钟！在理论上，RSA已经被量子计算机攻克了！

不过这只是理论上，因为真正能用的量子计算机还没有造出来。到目前为止，在实验上分解的最大的数是291,311 = 523 × 557，是由中国科学技术大学的杜江峰院士和彭新华教授等人在2017年实现的。这离分解上千位的密码还远着呢。

量子计算机是当前全世界的科研热门。许多研究机构和企业在激烈地竞争，纷纷放出风来要在近年内实现“量子制霸”，实际意思就是前面说的，对于某些问题超越现有的经典计算机。有发展的眼光的人，都会关注这方面的消息。

显然，量子计算的进步，增加了人们对量子密码术的需求。但是，如果没有量子因数分解算法，甚至压根没有量子计算机的概念，量子密码术是不是就没有价值了呢？

当然不是！

量子密码术的基本价值来自它的完美安全性，这是其他任何密码体系都没有做到的。无论计算技术有没有进步，这个价值始终存在。量子因数分解或者任何其他的计算技术进步，只是起到锦上添花或者说“补一刀”的作用，对这个基本图景并没有影响。

徐令予老师在文章中说：

“为什么要开发量子保密通信技术？因为从理论上讲，如果未来量子计算机建成，如果建成的量子计算机有足够的Qbit和足够的稳定性，那么今天密码系统中的公钥密码RSA有可能被破解。”

根据以上的分析，我们知道这个理解是错误的。实际上，最早的量子密码术协议BB84是在1984年发明的，而量子因数分解算法是在10年之后的1994年发明的。难道在1994年之前，人们会觉得BB84协议没有意义吗？

《后量子RSA》说了些什么？

徐老师在文章中对这篇论文的介绍是：

“数月前出现这样一篇论文：‘后量子时代的RSA’[2]，该文发表后被多家相关杂志转载和引用，这些文章给出的共同结论是：目前使用的非对称性密码RSA不会因为量子计算机的出现而消亡。”

如前所述，经过饶有兴味的研读之后，我大致理解了此文的框架。此文的四位作者Daniel J. Bernstein、Nadia Heninger、Paul Lou、Luke Valenta（以下简称为BHLV）表现出了很强的数学功力和创意，令我十分敬佩。那么，BHLV实际说了些什么呢？

他们说的是：目前版本的RSA在量子算法面前不堪一击，他们提出了一种改进的版本，在某种意义上可以对抗已知的量子算法。

在什么意义上呢？合法用户加密解密也是需要计算量的，而肖尔的量子算法强大到了这种程度：破解RSA跟合法用户解密几乎一样快，具体而言，计算量都大约是n的平方（n是要分解的那个合数的二进制位数）。对RSA密码体系来说，这简直是输得连底裤都快没有了。

传统的RSA是把两个质数相乘。BHLV提出，通过一系列数学技巧（快速的乘法以及随机生成质数的方法等等），可以把加密解密的计算量都控制在正比于n，然后把非常多的质数相乘，使得n非常大，就可以让破解的计算量显著地超过加密解密的计算量。简而言之，就是把加密解密的计算量（n）降低到了破解的计算量（n的平方）之下。他们把这种改进版RSA称为后量子RSA。

呃……原来我们说的是，破解的计算量指数增长才算安全。现在标准降得这么低，破解的计算量比加密解密增长得快就算安全，——这几乎是可以定义的最低级别的安全性了。

原文对此说得很清楚：

“Post-quantum RSA does not qualify as secure under old-fashioned security definitions requiring asymptotic security against polynomial-time adversaries. However, post-quantum RSA does appear to provide a reasonable level of concrete security.”

【翻译：在老派的安全性定义下，即面对多项式时间敌手时的渐近安全性的定义下，后量子RSA没有达到安全的标准。然而，后量子RSA看起来确实提供了一个合理水平的具体的安全性。】”

后面还有一个更具体的解释：

“Note that, for theoretical purposes, it is possible that (1) there are no public-key encryption systems secure against polynomial-time quantum adversaries but (2) there are public-key encryption systems secure against, e.g., essentially-linear-time quantum adversaries. Post-quantum RSA is a candidate for the second category.”

【翻译：请注意，对于理论的目的，以下两点是有可能的：(1) 没有任何公钥密码体系在多项式时间的量子敌手的面前是安全的；但是(2)有公钥密码体系在比如说基本上是线性时间的量子敌手的面前是安全的。后量子RSA是第二类的一个候选者。】”

如果你看不懂，我来简单解释一下。给定问题的规模n，如果你允许量子计算机运行对n的任意高阶多项式的时间，那么大概所有的公钥密码体系都会被击败。而如果你只允许量子计算机运行n的时间，那么就可能有公钥密码体系扛得住。后量子RSA是后一类中的一个候选者。为什么只说是候选者，而不是直接就是呢？因为你无法保证人们不发展出新的量子算法甚至是经典算法，在n的时间内破解后量子RSA。

从破解跟解密一样快，改进到加密解密比破解快，这个进步好比赢回了一条底裤。或者这么说：一个低手跟一个高手下围棋，从分先到让先，到倒贴目，到让二子，到让三子，一路被打得降级，现在提高了棋艺，在让三子的情况下赢了一盘，回到了让二子。这当然可喜可贺，不过如果把这理解成他可以跟高手分庭抗礼，甚至超过了高手，那就大错特错了。

用网络语言说：BHLV对RSA使用挽尊卡，为RSA挽回了尊严！效果：密码术经验+5。

对于后量子RSA的价值，原文有一个生动的比喻：

“RSA has enough flexibility to survive the advent of quantum computers — beaten, bruised, and limping, perhaps, but not dead.”

【翻译：RSA有足够的柔韧性来挺过量子计算机的来临——被打击，被挫伤，一瘸一拐地走，都有可能，但不是死亡。】”

再来看看BHLV用什么样具体的例子演示后量子RSA。目前常用的RSA是用两个质数相乘，每个质数用二进制表示是1024位或2048位。他们生成了2的31次方（2,147,483,648，即大约21亿）个质数，每个质数用二进制表示有2的12次方（即4096）位。这21亿个质数乘起来，得到了2的43次方（8,796,093,022,208，即大约8.8万亿）长度的一个密钥，也就是1 T字节长度的一个数字。想想看1 T容量足够放下多少部电影，现在居然只是用来存放一个数字！

处理如此巨大的数字，加密解密当然也很不容易。生成21亿个随机的质数，花费了一个1400核的机群4个月的时间。看起来这是最耗时间的一步，后边的质数相乘、加密、解密等步骤，花费的时间都是以天计，而不是以月计的。徐老师的文章说“费时一共为五天”，大概是只看了其中的一步。

根据BHLV的估算，肖尔的量子算法分解这个1 T字节长度的数字，需要的量子比特操作数是2的100次方。2的43次方平方就得到2的86次方了，再考虑到其他一些细节，2的100次方是可以理解的。徐老师在这里似乎出现了一个硬伤，把量子比特操作的数目看成了量子比特的数目，然后以此为根据做了一番讨论：

“假设量子计算机已经建成，再假设量子计算机的量子位（Qbit）可以无限扩展，进一步假设该量子计算机的运行成本与现在通用电子计算机的成本可以相比，用这样一台超级想象出来的量子计算机来破解长度为Terabyte（太字节，等于1024 GB）的RSA非对称密钥需要量子计算机的Qbit为2^100（2的100次方）。

2^100是一个什么概念？这个数大于我们星球上所有生物细胞的总数！而今天为了建成两位数Qbit的量子计算机，专家们已经弄得焦头烂额，多年来一筹莫展。当然使用长度为Terabyte的RSA公钥确实也有点离谱，但论文作者在今日的电子计算机上产生了这样的公钥，并用它来加密和解密，费时一共为五天。按目前的技术水平，长度为Terabyte的RSA公钥虽然并不实用，至少还是可以实现的，但是还在纸上的量子计算机即使明天就建成，要破解这样的RSA公钥也无一线希望。”

其实原文是“2100 qubit operations”，不是“2100 qubits”。这个错误的性质，相当于认为一个量子比特只能操作一次，然后就报废了。这当然是不对的。因此，拿2的100次方去跟细胞的总数相比，跟专家想建成多少位的量子计算机相比，都对错号了。

BHLV对2的100次方这个数字，仅仅是说它“惊人”（astonishing），没有像徐老师这样做这么多引申。这确实是一个非常大的数，但能不能说量子计算机做不了这么多操作呢？这话谁都不敢说。至于将来算法改进，在更短时间内破解后量子RSA的可能性，自然也无法排除。因此，后量子RSA正如BHLV所言，提供的是“一个合理水平的具体的安全性”，还是“看起来确实提供了”，而不是能够令理论家满意的安全性水平，更不是完美的安全性。

如何理解后量子密码学？

徐老师的文章中有这样一段：

“再让我们看看密码学界最近的动态，请先看下图：密码学界已经明确把公钥密码系统分成两大类，左列中都是目前常用的公钥密码，它们是‘量子可破’的，即理论上在量子计算机攻