根据联合国教科文组织2023年大会决议, 2025年被确立为“量子世纪年”或者“国际量子科技年”(International Year of Quantum Science and Technology),以纪念量子力学创立一个世纪以来的发展(recognizes 100 years since the initial development of quantum mechanics),2024年2月,活动被正式宣布。(https://quantum2025.org/)。
19世纪60年代,在一大批物理学家的电磁学工作基础上,麦克斯韦(James Clark Maxwell)将电磁学规律总结成一组方程,进而得到电场和磁场的波动方程,预言了电磁波,而且证明电磁波速度就是光速,所以推测光波的本质就是电磁波。
▲ 麦克斯韦。图源:维基百科。
麦克斯韦告诉我们,电磁波是电场和磁场共同在空间的传播。电场和磁场都在振动,频率(单位时间的振动次数)一样,相互伴随,互相垂直,又都与传播方向垂直(参见下图)。这些性质后来都得到了实验的证实,也使得光的波动理论更为细致。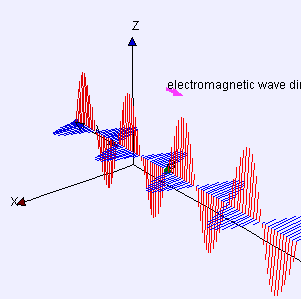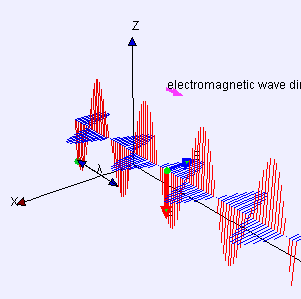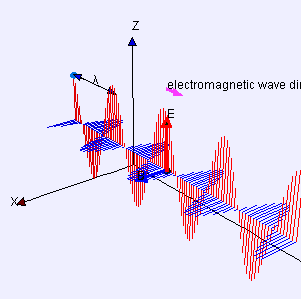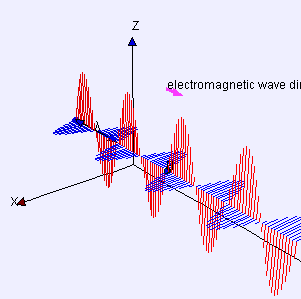
▲ 电磁波动画。图源:维基百科。
20世纪著名物理学家费米(Enrico Fermi)曾给新婚妻子劳拉·卡彭(Laura Capon)推导“电磁波的速度等于光速”,然后说:“所以光就是电磁波。”劳拉不接受,因为速度相等不代表就是同一个东西。她是对的,只能说“光波是电磁波”先是一个推测,后来得到了实验证实。偏振是在光学现象中首先发现的,但是在电磁理论中,得到清晰的解释:偏振方向就是电场方向。电场的方向总是垂直于光的传播方向,所以偏振总是垂直于光的传播方向,也就是说,电磁波是横波。在此前提下,仍然有各种可能性,就好比时针总是垂直于转轴,但是可以指向钟面上的不同方向。在垂直于传播方向的平面上,偏振(也就是电场方向)可以总是沿着某个方向,这叫做线偏振。偏振也可以随时间变化,但是电场、磁场、传播方向总是保持两两互相垂直,比如圆偏振和椭圆偏振。自然光没有偏振,可以看成任意一对垂直方向的偏振光的等量混合。以前的波(比如声波、水波)都是媒介振动的传播,那么电磁波的媒介是什么?人们长期认为是无处不在的以太,但是却从未观察到地球或其他天体对以太的扰动。19世纪早期,阿拉果就发现,地面光源发出的光和天体发出的光都反映,地球似乎相对以太静止。菲涅尔猜想,这是因为光被拽着一起运动,菲索(Hippolyte Louis Fizeau)和爱里(George Biddell Airy)的实验似乎都证明这一点。麦克斯韦也这么认为,他在论证麦克斯韦方程组时,设计了以太的机械模型,《大英百科全书》第九版中的“以太”条目就是他写的。他还在一封信中,提出测量以太相对于太阳系的速度的方法,与罗默确定光速的方法有关,以木卫一食(木卫一被木星挡住太阳光)作为观察目标。在地球上观测到木卫一食需要一定的时间延迟。假设以太存在,那么太阳系相对以太的速度在太阳—木星连线上有个分量(记作v)。木星位于太阳(下图中的A)和地球连线的延长线上时(下图中的A’),木卫一反射的光相对于太阳系的速度等于光相对以太的速度(就是光速c)加上这个速度份量v,即c+v。半年后,木星位置改变可忽略(因为木星绕太阳一圈需12年),而地球绕到木星—太阳连线的延长线上(下图中的B),所以木卫一要被地球上的人观测到,需要更长的时间延迟,因为路程增加了地球绕太阳的轨道的直径d。两种情况的时间差就是d除以光相对于太阳系的速度c+v,即d/(c+v)。6年以后,木星到了绕太阳轨道的另一侧(B’),木卫一发出的光相对于太阳系的速度是c-v,两种情况(一是地球在太阳—木星连线上,另一是地球在太阳—木星连线延长线上)的时间差是d/(c-v)。这两个时间差的差别是2(d/c)(v/c),正比于太阳系相对以太的速度与光速之比v/c,。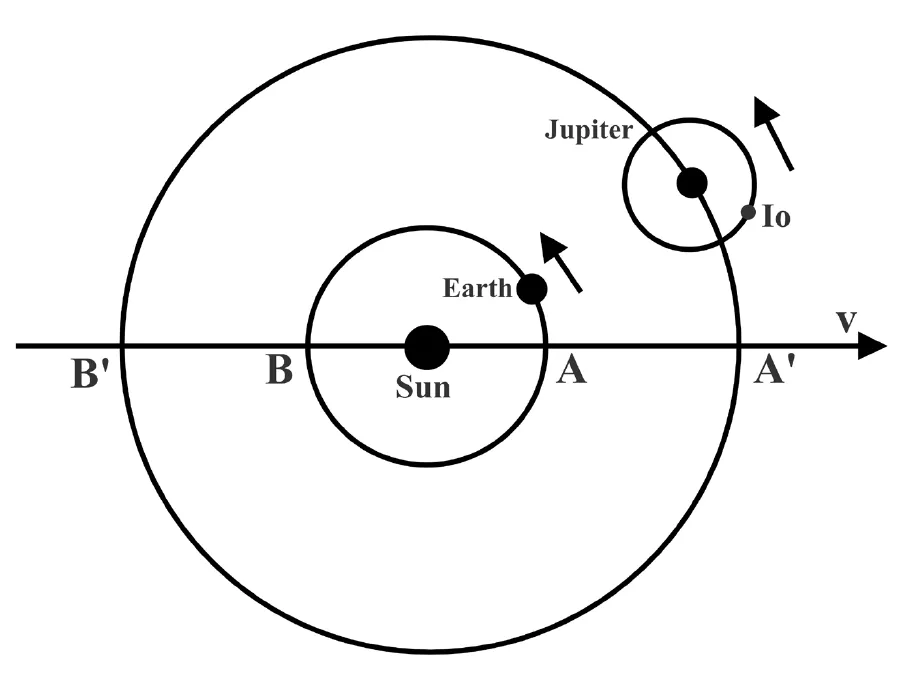
麦克斯韦去世后,这封信被发表于Nature(自然)杂志,激励了迈克尔逊(Albert Abraham Michelson)开始用迈克尔逊干涉仪,通过光的干涉,测量以太相对于地球的速度v。光分别沿着和垂直于v方向,传播相同距离l,再原路返回,发生干涉,时间差是(l/c)(v/c)2,所以是v/c的平方效应。而麦克斯韦的方法测量v/c的一次效应,敏感得多,但麦克斯韦用天体运动来测,毕竟不如实验室测量精确和方便。1881年,迈克尔逊和莫雷(Edward Williams Morley)宣布他们多次实验的结果:探测不到以太与地球的相对运动。1905年,爱因斯坦发表狭义相对论,指出光相对于任何惯性系的速度都是一样的。因此迈克尔逊-莫雷实验等一系列与以太假设相关的实验都可以得到解释:不需要假设以太的存在,电磁波本身就是一种实体。回到1665年,牛顿用三棱镜色散实验获得了太阳光谱。这可以看成第一个光谱学实验。光谱是指混合光中,各种单色光的分布。1748年,梅尔维尔(Thomas Melvill)将几种物质放在酒精灯中燃烧,观察到光谱中出现一个明亮的黄线,这就是钠元素的光谱线。1800年,赫谢耳(William Herschel)发现太阳光包含不可见的红外光,而且发现,热在太阳光谱中的不同颜色的分布不均匀。他认为红色的最热(81年后,人们发现,并不是红色的最热)。1802年,沃拉斯顿(William Hyde Wollaston)在太阳光谱中观察到几条暗线。1814年,夫琅和费(Joseph Fraunhofer)在若干灯光中发现钠线,而且看到很靠近的双线,他又在太阳光谱中发现了大量暗线,被称为夫琅和费线。光谱线的原理要等到量子力学来解释,双线结构是弱的自旋轨道耦合导致。
▲ 夫琅和费。图源:维基百科。
下面两个图分别是夫琅和费和当代科学家得到的太阳光谱。
▲ 夫琅和费得到的太阳光谱。图片来自网络。
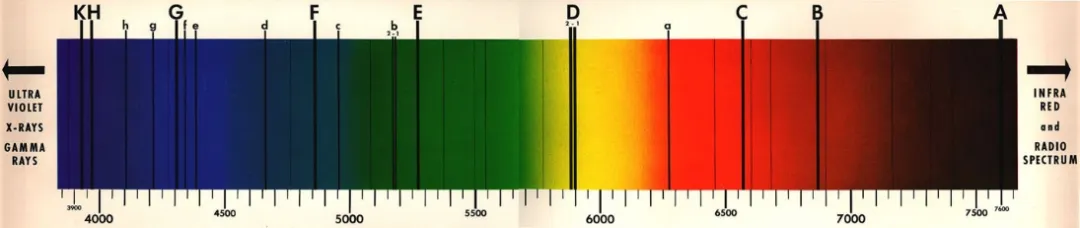
▲ 当代科学家测量的太阳光谱。图片来自网络。
1832年,布儒斯特描述了光线经过有色玻璃或气体所形成的暗线光谱。稍后,米勒(William Allen Miller)和傅科(Jean Léon Foucault)分别确定,钠的明线和太阳光谱的D暗线(参看上图)严格符合,因此他们想到,夫琅和费线可能是太阳大气的吸收造成,但没有得到确认。1842年,多普勒(John Christian Doppler)提出光波与声波类似,频率随着光源的运动而改变,即多普勒效应。1859年,基尔霍夫(Gustav Robert Kirchhoff)和本森(Robert Wilhelm Bunsen)指出,太阳光谱中的黑线由太阳大气中的物质导致,而同样的物质如果处于火焰中,就会在光谱中的相同位置(相同频率)产生明线。这就是我们今天所知的吸收谱线和发射谱线。他们提出在太阳光谱中找到了钠、镁、铜、锌、钡、镍的谱线,并用光谱确定金属的存在,以此方法在某种矿泉水中发现了铯和铷。
▲ 基尔霍夫。图源:维基百科。
1862年,塞曼(Pieter Zeeman)发现磁场使得光谱线发生劈裂。这就是我们现在熟知的塞曼效应。1868年,哈金斯(William Huggins)发现太阳转动引起谱线移动。后来,基于多普勒效应导致的光谱移动,天文学家做出一系列发现,包括双星、土星环的非整体性以及恒星运动的不同速度。1868年,埃格斯特朗(Anders Jonas Ångström)发表太阳光谱中的各个波长的表。Ångström(埃)后来成为长度单位,代表10-10米。1881年,兰利(Samuel Pierpont Langley)发现太阳光中的蓝光和绿光被大气吸收得多,因此变白。他测定了太阳光谱的很多红外谱线。1884年,巴尔末(Johann Jakob Balmer)根据4条氢光谱谱线,总结出一个波长公式,即波长正比于一个自然数的平方除以它减去2的平方。今天,这些谱线称为巴尔末线系。
▲ 巴尔末。图源:维基百科。
下图是今天我们了解的氢原子光谱,从中可以看到巴尔末线系(n=2)。n现在叫做主量子数,对应于电子沿着与原子核连线方向运动的量子态和能量。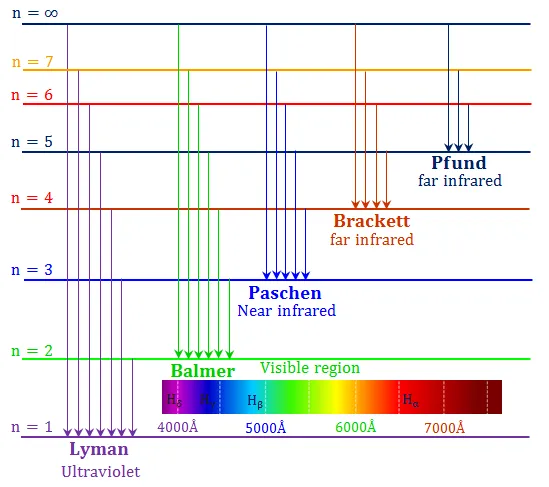
▲ 氢原子光谱。图片来自网络。
1890年,里德堡(Johannes Robert Rydberg)独立提出一个波数公式,与巴尔末公式一致,但是适用于不同谱线系。1894年.帕邢(Friedrich Paschen)将太阳光谱的红外区从兰利的5微米扩大到9.3微米,1897年又扩大到23微米。1895年,伦琴(Wilhelm Conrad Röntgen)发现x射线。他用x射线给他的夫人照了照片。参见下图。伦琴认为它是以太的纵波,斯托克斯(George Gabriel Stokes)认为它是电磁波的脉冲,这是最早将x射线与电磁波联系。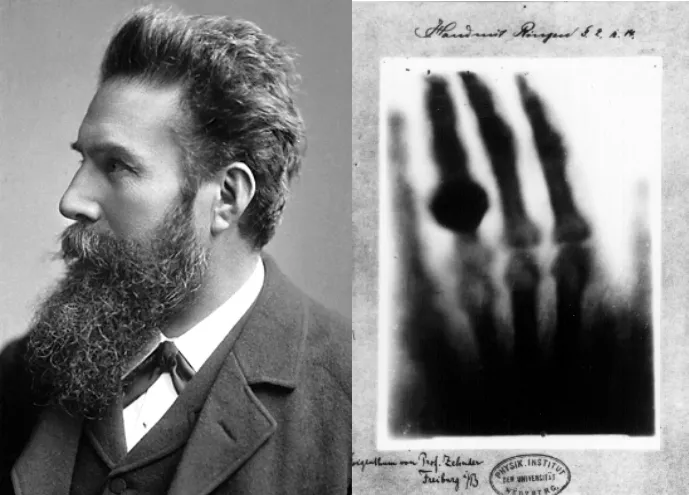
▲ 左:伦琴,右:他的夫人的手的x射线照片。图源:维基。
1906年,莱曼(Theodore Lyman)发现波长1000埃的紫外线。1908年,里兹(Walther Ritz)提出组合规则,即光谱线频率正比于两个自然数平方倒数的差,比例系数后来叫做里德堡常数,之前已经出现于里德堡的公式。帕邢同年做了些验证,他发现第一个自然数是3的谱线系,叫做帕邢线系。里兹公式中第一个自然数为2的线系是巴尔末研究的,叫做巴尔末线系。第一个自然数为1的线系是紫外线,是莱曼发现的,叫做莱曼系。参见上面的氢光谱图片。1912年,劳厄(Max von Laue)等人发现x射线被晶体衍射。这说明x射线的波长与晶体重的原子间距接近。不久,布拉格父子(William Henry Bragg 和William Lawrence Bragg)发展了x射线晶体学。人们了解到,x射线是电磁波。
▲ 劳厄1912年发表的x射线衍射图。
本来人们所说的光是可见光,后来就不区分光和电磁波了。电磁波的频率决定了无线电波、微波、红外线、可见光、紫外线、X射线、伽马射线的区别,也决定了可见光的颜色。真空中,所有的电磁波的速度都一样,也就是光速,光速乘以频率就是波长,是一个振动周期内光传播的距离。整个电磁波谱也称为光谱。1926年,密立根(Robert Andrews Millikan)说:“过去两年,用于不可见以太波的新实验技术已经完全消除了人工电磁波和热波之间的鸿沟。”这里也反映了密立根没有放弃以太的说法。物体保持一定温度,即达到热平衡时,电磁辐射(简称辐射)是各种频率电磁波的混合,而且能量分布与物质结构无关,称为热辐射。温度不太高时,辐射基本上都不可见;随着温度的升高,物体发红;温度更高时,物体发白。辐射落在物体上,有反射,有吸收,物体自身也发射辐射。热辐射的研究需要结合电磁学与热力学和统计物理。
▲ 黑体颜色随温度的变化,横坐标的单位是绝对温度。
1859年,基尔霍夫提出热辐射的基尔霍夫定律:物体的发射本领与吸收本领之比只取决于温度和频率,是一个与物体无关的普适量。某个频率的发射本领是单位时间单位面积发射的该频率辐射的能量谱密度。可以证明,发射本领等于辐射本身的能量谱密度乘以1/4的光速。它对于频率的积分给出单位时间单位面积发射的总能量。吸收本领则是单位时间落在物体单位面积上的辐射被吸收的比例。吸收本领为1的物体叫做黑体,也就是说,黑体只有吸收和发射,没有反射。因此将基尔霍夫定律用到黑体,得到普适量就是这个频率的黑体辐射能量谱密度乘以1/4的光速。实验上直接测量的是辐射强度,即单位时间单位面积单位立体角辐射的能量谱密度,等于发射本领除以π,也就是黑体辐射能量谱密度乘以光速除以4π。1879年,斯特番(Josef Stefan)给出一个经验规律,物体单位时间单位面积发出的总能量正比于温度的4次方。这是有缺陷的,因为只有黑体才有这个规律。1881年,兰利发现,太阳光谱中最热的部分是橙色,而不是红色。1884年,玻尔兹曼(Ludwig Boltzmann)从理论上证明,黑体满足斯特番定律。1893年,维恩(Wilhelm Wien)从理论上提出,辐射的能量谱密度(正比于辐射强度)等于频率的3次方乘以一个频率除以温度的函数,由此验证了斯特番定律,并推导出维恩位移定律:给定温度下,辐射强度作为波长的函数,最大值对应的波长与温度的乘积是一个常数。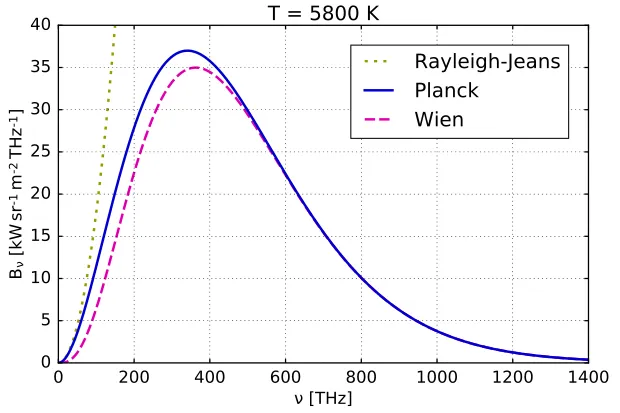
▲ 黑体辐射的辐射强度的几个公式的比较,普朗克(Planck)公式与实验完全一致。
1895至1901年,卢默(Otto Lummer), 普林舍姆(Ernst Pringsheim), 库尔班(Ferdinand Kurlbaum),鲁本斯(Heinrich Rubens)测量了黑体辐射在不同频率的辐射强度,给出了对频率的依赖关系,与温度有关,并证明了维恩定律。1900年6月,斯特拉特(John William Strutt),也就是瑞利勋爵(Lord Reyleigh),使用能量均分定理(每个自由度的平均动能是RT/2N,T为温度,R是理想气体常数,N是阿伏伽德罗常数,后来人们定义R/N为玻尔兹曼常数),得到能量谱密度(正比于辐射强度)。用波长表示时,它正比于温度除以波长的4次方;用频率表达时,它是温度乘以频率的平方。对于短波长(或者说高频率),这个理论结果与实验偏离很大。为了消除这个紫外灾难,他乘上指数衰减因子。1900年10月7日傍晚,鲁本斯将他覆盖整个频率范围的最新实验结果告诉普朗克(Max Planck)。普朗克当晚就提出一个与最新实验一致的能量谱密度公式,适用于各种频率,是频率和温度的函数,推广、结合了以前低频率和高频率的公式,也就普朗克定律。接着的两个月里,他从理论上推导出这个公式。他没有用能量均分定理,而是从普朗克公式反推,提出关于黑体辐射的量子假设,开启了量子论[7,8,9]。当温度除以频率(或者说温度除以波长)很大时,普朗克公式退化为瑞利公式。根据麦克斯韦的电磁理论,辐射来自做振动的带电粒子,简称振子。当时对物质结构所知有限,不去追究带电粒子具体是什么。好在结果普适,与具体结构无关,实验结果也是如此。普朗克的理论推导基于量子假设:每个振子的能量总是某个基本单元的整数倍,这个基本单元叫做能量量子,等于一个常数乘以频率,后来人们称此常数为普朗克常数。既然普朗克的振子能量是量子化,那它们发射和吸收的电磁波能量也是量子化的,一份一份的。普朗克当初称普朗克常数为作用量量子,因为它的量纲是作用量的量纲,也就是能量乘以时间的量纲,后来人们称之为普朗克常数。这里的“量子”(quantum)有不可分割的基本单元的意思,好比货币有个基本单元(1分钱)。普朗克常数的数值是h=6.62607015×10-34J·s=4.13566743(35)×10-15eV·s,这里J代表焦耳,eV代表电子伏特,s代表秒。2021年起,每年的4月14日被定为“世界量子日”。
▲ 普朗克与爱因斯坦。
1905年,爱因斯坦(Albert Einstein)发表《关于光的产生和转换的一个启发性观点(On a Heuristic Point of View about the Creation and Conversion of Light》。他先指出普朗克的量子论之所以成功,是因为抛弃了能量均分定理,接着又更进一步,提出光量子理论,指出电磁波本身就是由很多很多一个一个的能量量子构成,叫做光量子[7,8,10]。也就是说,爱因斯坦将量子假说用到电磁波本身,指出“光量子”是光的不可分割的单元。在这篇论文中,作为光量子假说的应用,爱因斯坦解释了光电效应,并提出了光电效应定律。论文还讨论了光致发光,分为荧光和磷光,前者符合量子力学选择定则,所以立即发生;后者如果直接发生,则违背量子力学选择定则,所以需要复杂的中间过程,从而时间尺度长。荧光和磷光是人类自古以来就观察到的现象,但是它们的机理需要等到量子论来解释。公元前100多年的《淮南子》写道:“老槐生火,久血为磷”。公元前100年左右的《礼记》记载:“腐草为萤”。16世纪的李时珍可能已经知道磷光和荧光不同。一个普遍误解是,以为爱因斯坦1905年就提出,光量子是一个量子粒子,以光速运动,有动量。事实上,1905年的时候,爱因斯坦只是说光量子是能量量子,并没有说它具有动量。1916年,爱因斯坦才提出光量子具有动量。当时,他提出辐射理论(为几十年后的激光打下最初的基础),分析了辐射和分子气体的热平衡,指出:“当一束辐射引起分子发射或者吸收能量hν,那么就有动量hν/c传给分子,对于吸收的情况,动量方向与那束辐射的方向相同;对于发射,动量方向与那束辐射的方向相反。”[7,11,12]至此,爱因斯坦才表明光量子具有全面的粒子性质,既有能量,也有动量,它们都与频率成正比,反映了也具有波动性。后来人们称之为“波粒二象性”。光量子的动量增加了爱因斯坦对光量子假说的信心,正如他在给朋友贝索(M. Besso)的两封信中所说。一封信中写道:“这样,光量子的存在性实际上肯定了”,另一封信中写道:“我不再怀疑辐射量子的实在性,虽然我在此信念上还很孤独。”[7]1925年,莱维斯(Gilbert Lewis)发表了一篇文章,标题是“光子的守恒(Conservation of photon)”,提出“光由一种新的原子,不可产生,不可消灭,命名为光子”。他所说的“光子”本意并不是爱因斯坦的“光量子”,文章观点也是不对的,并未引起重视,但是人们从此采用“光子”这个名词作为爱因斯坦的光量子的简称,沿用至今。1927年索尔维会议的议题就是“电子和光子”。300多年前,牛顿就说过光由微粒构成。但是他的微粒是经典粒子,像玩具小球一样,服从牛顿定律。光子也有很多类似的粒子属性,比如具有运动的速度,也就是光速,也有动量,等于能量除以光速,质量等于0,符合狭义相对论。光子概念很好地结合了量子论和狭义相对论的思想。光子也可以有其他内禀性质,比如偏振。多年以后,类似的概念拓展到基本粒子,包括理论上的引力子,以及凝聚态的激发,比如晶格振动的量子叫做声子。1897年,汤姆孙(Joseph John Thomson)发现电子。1923年卢瑟福(Ernest Rutherford)说:“很快人们看到电子肯定是所有原子的组成部分,光谱来自电子的振动。”1911年,卢瑟福提出原子由原子核和电子组成。1913年,玻尔(Niels Bohr)提出他的原子模型,其中电子在原子核的电场力作用下,处于特定的轨道,在不同轨道之间的跃迁伴随着光的发射或吸收,能量是普朗克常数乘以频率,由电子初末轨道的能量差决定。利用里兹组合规则,这反过来确定了不同轨道的能量。分立的轨道和能级也成了“量子化”的含义。索莫菲(Arnold Sommerfeld)将电子轨道从圆形推广到椭圆。后来,发出光的电子初态和末态也从原子外的轨道推广到其他情况,比如分子或者凝聚物质中的电子态。我们今天将这些发出的光直接说成光子,但是玻尔当初并没有这个意思,因为他直到1925 年康普顿效应中的能量动量守恒被证实后,才接受光子说[8]。
▲ 玻尔与索莫菲。
光谱在量子论和量子力学的发展中扮演了至关重要的角色,在很多领域一直很重要,成为探测原子、分子、凝聚物质等系统中的电子态的重要手段,也是研究天体物理的重要途经,例如,获得2019年诺贝尔奖的太阳系外行星和获得2020年诺贝尔奖的银河系中心的超大质量致密物质的信息都是来自光谱。量子论后来发展为系统的量子力学,最关键的理论工作完成于1925年左右(我们将另文评述这段时期的量子力学发展)。光子服从量子力学的规律,比如它的运动具有随机性,由概率描述。这个概率是波函数的大小的平方,而波函数在空间的分布就像波一样,所以,由很多光子组成的光就有了光波的性质。量子力学经受了无数实验检验,用来描述我们不能直接感知的微观世界。量子力学的描述是概率性的。很少人了解,正是爱因斯坦首先在量子论中注意到概率的不可避免。他指出,自发辐射导致分子吸收或者发射光量子,而光量子的方向是随机的。爱因斯坦预感到,这些过程使得关于辐射的真正的量子理论不可避免[11,12]。量子论中的其他自发过程也是类似地具有随机性。所以爱因斯坦首先将概率引进到量子论,虽然后来他又因为概率成为基本特性而感到不满意。光的性质可以归结为光子的性质,所以光子也有偏振,理论上对应于电场的量子化,可以通过透光方向与偏振方向一致的偏振片。光子的偏振可以当作一种内禀状态。偏振正交的量子态可以组合成自旋(与轨道运动无关的内禀角动量)的本征态(意思是有确定的自旋),自旋量子数(确定值,以普朗克常数除以2π为单位)为1。通常量子数为1的自旋有3个本征态,但是光子没有质量,不存在静止参考系,因此转动对称性不是全空间的,而是绕着运动方向,从而只有两个自旋本征态,这也叫螺旋度的本征态。现在假设我们有一个光子,但是不知道它的偏振状态,那么如何来测量呢?量子力学告诉我们,测量光子偏振的仪器给光子规定了两个互相垂直的方向(都垂直于运动方向),专业名词叫基(basis)。这就好比时钟上0点和3点的方向,或者1点和4点的方向,如此等等,而光子运动方向对应于时针的转动轴。奇妙的是,光子经过测量后,偏振就变成这两个方向中的一个。变成哪个呢?这是随机的,有一定的概率分布,取决于原来的偏振方向与测量方向的夹角,也就是马吕斯定律中的投射强度与原强度之比换成概率。只有碰巧当这两个互相垂直的测量方向之一与光子原来的偏振方向一致,光子偏振才不变。所以,如果不知道光子偏振方向,随便用一对互相垂直的方向去测量,那么除非碰巧这两个方向之一与光子原来的偏振方向一致,一般情况下,测量改变光子。利用这个原理,可以设计量子密码。密码的关键是密钥,是一串数字。我们可以将一个讯息表示成一串2进制数字(非0即1),然后与一串密钥一一相加,规则是1+0=0+1=1,0+0=1+1=0。比如,假设原来的讯息是10011010,密钥是01010100,那么加密后的讯息就是11001110。解密时,将加密讯息再加上这个密钥即可。因为1+1=0+0=0,所以加两次密钥就抵消了。量子密钥本身仍然是一串数字,只是产生的方法是量子的,所以叫做量子密钥分发。如果中途有人窃听,按照上面所讲的道理,很可能改变了光子。这样,就可以检测到在传输过程中是否有人“窃听”了信息。一个常用方案是本纳特(Charles H.Bennett)和布拉萨德(Gilles Brassard)于1984年提出的,被称作BB84方案[13,14]。举例如下。张三先随意确定一个数字,0或者1,然后用光子偏振代表,既可以用某一对垂直的方向代表,也可以用另一对垂直方向代表,张三随机在这两对方向中选择一对。然后将光子发给李四。李四收到后,也随机用这两对方向中的一对去测量。然后两人交流,各自用了哪一对方向。这个交流可以公开,因为只交流用了哪一对方向,并不透露实际测量结果。如果两人用了同一对方向,李四就留下光子。如果光子传输途中没有受到干扰,李四的测量之后的光子状态应该就是张三发出时候的光子状态。但是如果中途有人窃听,按照上面所讲的道理,很可能改变了光子。那么,即使李四所用的一对方向与张三当初所用的那一对方向一样,测量出来的光子状态也可能不是原来的状态。这就是出错。张三和李四用这样的方法传送很多光子,并交流每个光子发出时用哪一对方向,测量时用哪一对方向,留下两人用同一对方向的光子。然后再牺牲一部分光子,作为抽样,拿出来分析有没有被窃听。两人交流这些光子在每人手上时的状态(公开测量结果),用来分析不一致的比例。如果比例达到一定的大小,就说明有人窃听过。否则就说明没有人窃听,可以用余下的光子状态作为密钥。还有一个基于量子纠缠的量子密钥分发方案。在量子力学里,几个粒子彼此相互作用后,量子特性成为整体性质,无法单独描述各个粒子的量子性质,只能描述整体系统的量子性质。这种情况被称作量子纠缠,是一种纯粹发生于量子系统的关联[14]。在经典物理里,不存在这种情况。对于一对量子纠缠的光子对,无论相距多远,如果纠缠没有被破坏,只要测量了其中一个的状态,测量者如知道原来的纠缠态,就可以知道另一个的状态(但是其他人不知道)。在此基础上,有如下密钥生成方案。张三和李四之间分享很多对量子纠缠的光子对,在此基础上,他们之间不需要再传送光子,也可以产生密钥。在地面上,通过光纤或者自由空间,已有很多量子密钥分发的实现。2017年以来,潘建伟团队用“墨子号”量子卫星实现了各种量子密钥分发 [15]。他们先是在卫星和地面之间,以及作为中继在中国和奥地利之间,实现了BB84方案;又用卫星向相距1120公里的两地分发量子纠缠的光子对,以此为基础生成密钥(下图);还进行了基于量子纠缠的各种实验[15]。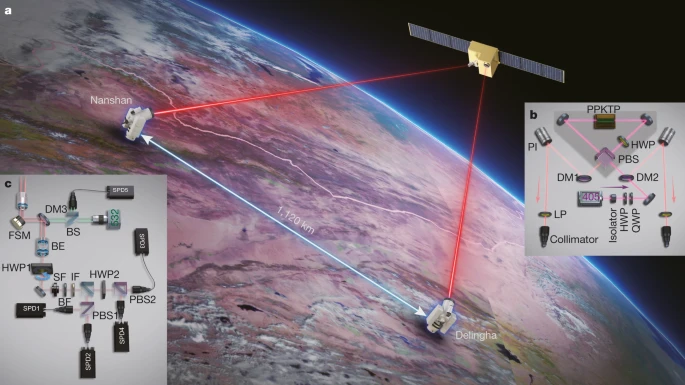
▲ 2020年,墨子号量子卫星在相距1120公里的两地(德令哈和丽江)之间实现基于量子纠缠的密钥分发。图源:https://www.nature.com/articles/s41586-020-2401-y。
“墨子号”量子卫星(参见下图)2016年8月发射,质量631千克,在太阳同步轨道运行,卫星搭载了量子密钥通信机(信号光是可调制波长850纳米的弱相干光源)、量子纠缠发射机(可产生波长810纳米的纠缠光子对)、量子纠缠源、高速相干激光通信机、量子实验控制与处理系统[16]。量子密钥通信机包括一台Cassegrain望远镜, 口径300毫米,可做小范围调节,借助卫星姿态对准地面站。量子纠缠发射机包括另一台Cassegrain望远镜, 口径为180毫米,具备两轴大范围调节能力,能独立跟踪对准地面站。光机主体也包含信标光系统以及跟踪捕获系统。卫星也装载用于两个产生脉冲同步光的532nm脉冲激光器。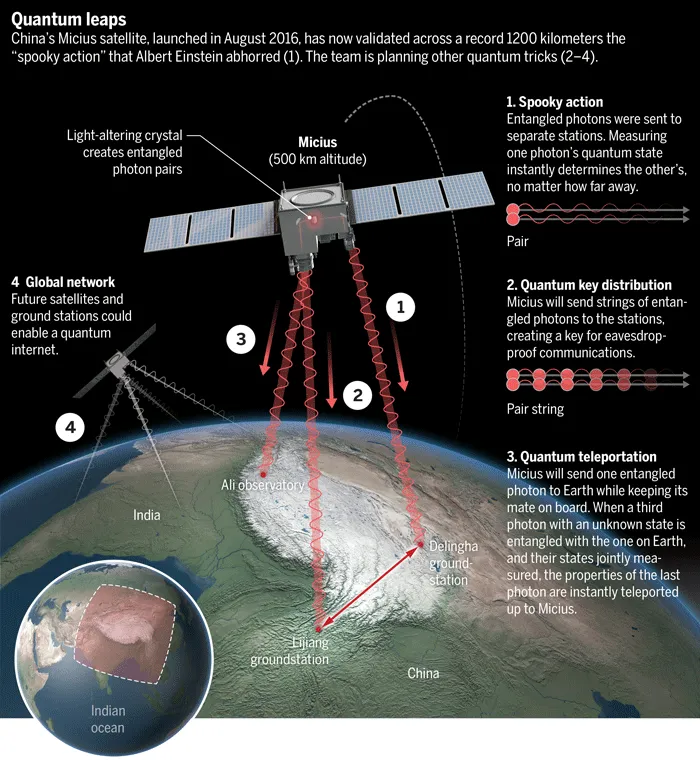
▲ Science(科学)杂志对墨子号量子卫星的介绍。图源:https://www.science.org/content/article/china-s-quantum-satellite-achieves-spooky-action-record-distance
中国的从事光学操控的量子卫星被命名为墨子号,正好纪念了墨子及其门徒对光学以及物理其他方面的极早期探索。2022年诺贝尔物理学奖授予阿斯佩(Alain Aspect)、克劳泽(John F. Clauser)和蔡林格(Anton Zeilinger)。他们的获奖工作就是基于纠缠光子的贝尔不等式检验和量子信息科学奠基性贡献[17],诺奖委员会的官方文件和新闻发布会也都提到了“墨子号”卫星[18,19]。在量子计算研究中,光子也扮演了重要角色。例如,潘建伟团队的“九章”量子计算原型机用光子操控处理高斯玻色取样,先后操控了76个光子、113个光子和255个光子。基于255个光子,“九章三号”(下图)用1.27微秒算出的样本,如果用当前全球最快的超级计算机“前沿”(Frontier)去产生,约需300亿年,体现了量子优越性[20]。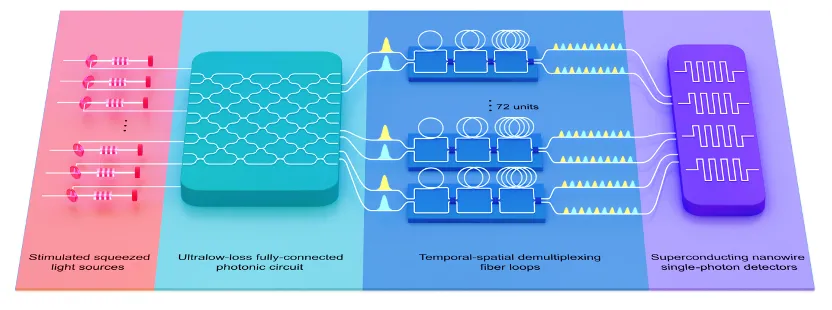
▲ “九章三号”实验装置[20]
在量子精密测量中,光子也是重要的工具。例如,潘建伟团队实现了超过200公里的远距离单光子三维成像 (下图)[21]。
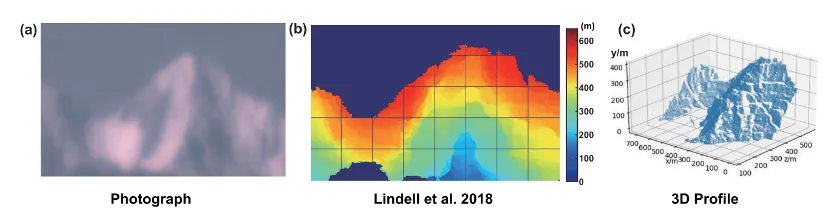
▲ 201.5公里成像结果(a)可见光照片,(b)前人的重建结果,(c)潘建伟团队的3维重建图[21]。
[7] A. Pais, Subtle Is the Lord, Oxford University Press, 1982.
[8] 施郁. 庆祝2015国际光之年、纪念早期量子论— 从2014 年诺贝尔物理学奖与化学奖谈起,现代物理知识,2015年27 卷1期,32-34。
[9] 施郁,绝路逢生生量子,墨子沙龙,2022-10-19.
[10] 施郁,整整100年前,爱因斯坦为何获得诺贝尔奖?2022-11-13
[11] A. Einstein, On The quantum theory of radiation, Mitt Phys Ges Zurich,18,47-62(1916).
[12] 施郁,爱因斯坦在1916: 从引力波到量子电磁辐射理论,科技导,34(8),107-112 (2016).
[13] C. H. Bennett and G. Brassard, Quantum cryptography: public key distribution and coin tossing, Proceeding of IEEE International Conference on Computers, Systems and Sigmal Processing, IEEE, New York, 1984.
[14] 施郁. 揭秘量子密码、量子纠缠与量子隐形传态,自然杂志,2016年38卷4期,241-247。
[15] C. Lu et al., Micius quantum experiments in space, Rev Mod Phys 94, 035001(2022).
[16] 国家空间科学数据中心,量子科学实验卫星—“墨子号”,https://www.nssdc.ac.cn/nssdc_zh/html/task/mozi.html
[17] 施郁. 量子纠缠之路:从爱因斯坦到2022年诺贝尔物理学奖,自然杂志,2022年44卷6期,455-465。
[18] The Nobel Committee for Physics,, How entanglement has become a powerful tool, Popular Science Background, Noble Prize in Physics 2022.
[19] The Nobel Committee for Physics, Scientific Background on the Nobel Prize in Physics 2022
[20] Y. Deng et al., Gaussian Boson Sampling with Pseudo-Photon-Number Resolving Detectors and Quantum Computational Advantage, Phys. Rev. Lett. 131, 150601 (2023).
[21] Z. Li, et al., Single-photon imaging over 200 km, Optica 8, 344-349 (2021).



